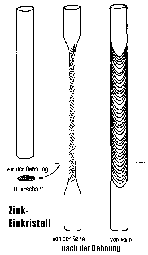|
Kernmechanisches Modell
Die klassische Quantenmechanik ist in den hundert Jahren seit ihrem Bestehen kontinuierlich und mit großem Erfolg weiter entwickelt und ausgebaut worden.
Verschiedene physikalische Experimente und Beobachtungen der letzten Zeit haben nun aber, wenigstens in Teilbereichen, zu Zweifeln an
bislang bewährten Modellvorstellungen der Physik geführt: So sagte etwa das klassische Schalenmodell von Goeppert-Maier, Haxel, Jensen und Süss1 den
nächsten “doppelt magischen” Atomkern nach dem bis jetzt letzten und schwersten derart klassifizierten Kern von Blei-208 (mit magischen 82 Protonen und dito 126 Neutronen) für ein aus 114 Protonen und
184 Neutronen bestehendes “superschweres” Element 114 voraus. Solch ein – in der Natur nicht vorkommendes – nach den radioaktiven Elementen Thorium und Uran zumindest ähnlich langzeitstabiles
bleiähnliches Element konnte aber trotz jahrelanger großer Anstrengungen nicht synthetisiert werden, während die tatsächlich durch Schwerionenbeschuß von Blei oder Bismut etwa mit Zink in eher unwägbaren
Mengen erzeugten Elemente 107 bis 112 in der Regel nur Millisekunden oder Bruchteile davon “lebten” (Ausnahme: E 108-269 = 9,3 s), bevor sie – meist durch das (wiederholte) Abspalten von Alpha-Teilchen –
in jeweils leichtere Kerne zerfielen.
Mittlerweile ist insofern hier jedoch eine andere Lage entstanden, als zunächst in einem russischen Labor in Dubna nunmehr
wahrscheinlich auch die Synthese des Elements 114 gelang, indem ein Target aus Plutonium-244 mit Kalzium-48-Ionen beschossen wurde. Nach dem “Abdampfen” von 3 Neutronen blieb dabei schließlich ein Kern des neuen Elementes 114 mit einem Atomgewicht von 289 übrig, welcher immerhin erst nach 30 Sekunden in das diesmal nun sogar 15 Minuten überdauernde Tochternuklid 112 zerfiel. Dieser Vorgang der Abspaltung jeweils eines Alpha-Teilchens wiederholte sich danach noch zweimal, bevor der Kern am Ende als Element 108 nach der Rekorddauer von 17 Minuten schließlich in kleinere Bruchstücke zerplatzte.
War dieses – bislang einmalige – Ergebnis für die Vertreter der bisherigen “klassischen” Schule der Schwerionenforschung in Deutschland2 und den USA schon einigermaßen überraschend bzw. unglaubwürdig, so verschärfte sich die Situation, insbesondere für das Schalenmodell, durch ein weiteres, inzwischen mehrfach wiederholtes Experiment noch
erheblich: Dem zuvor in Deutschland forschendem Physiker Victor Ninov (und seiner Arbeitsgruppe), der an sich nur die Theorie des polnischen Physikers Robert Smolantzuck widerlegen wollte, welcher das
Zentrum der gesuchten “Insel der Stabilität” erst bei einem Element 120 erwartete, gelang in Berkeley, USA, nunmehr durch den Beschuß von Blei-208 mit Krypton-86-Kernen relativ häufig die Synthese des neuen superschweren Elements 118, mit einer Lebensdauer von 0,2 ms, bzw. 0,6 ms für die beiden folgenden Kerne der Zerfallskette, die diesmal sogar bis zum Element 106 reicht.
Als Resultat all dieser Experimente ist infolgedessen die bisher so beruhigende Gewißheit des Schalenmodells zum einen einer großen
Unsicherheit gewichen, zum anderen aber auch einer großen Euphorie, die Insel der Stabilität – und sei es erst beim Element 120 (oder größer) – womöglich doch noch zu erreichen.
Demgegenüber hatte das Kernmechanische Modell 3, 4 bereits früher eine relativ stabile Kernstruktur für ein Atomgewicht von mehr als 272 vorausgesagt, verbunden allerdings mit einer deutlich geringeren
Halbwertszeit als der von Uran und wahrscheinlich auch von Fermium. Das obige Ergebnis der Forschergruppe um Juri Oganesjan in Dubna paßt also voll in dieses Bild und auch, daß der E-114-Kern nach drei
Alpha-Zerfällen bis hin zu A=277 anschließend zerplatzte, bzw. am Ende sogar zerplatzen mußte!
Ein anderes, ebenfalls “mechanistisches” Kernmodell, welches mit Clustern von Alpha-Teilchen, statt von Nukleonen
arbeitet und aus deren Anordnung ebenfalls Kernformen erschließen möchte5, trägt zwar der fest verwurzelten, wenn auch etwas naiv anmutenden Vorstellung mancher Physiker Rechnung, die die auffällige Bevorzugung der Zahl 4
in der Kurve der Bindungsenergie nun auch in Gestalt konkreter Alpha-Teilchen in den Atomkernen wiederfinden will. Das insbesondere mit den Namen Fred Hoyle und Kiyomi Ikeda verbundene Modell wurde
inzwischen weiterentwickelt und zeigte dabei eine evidente Übereinstimmung von Theorie und Messung bei Beryllium-8, ist aber dennoch seither nicht wesentlich über eine unsichere Beschreibung der
leichtesten Kerne bis etwa Magnesium-24 hinausgekommen. Wie das Kernmechanische steht auch das Alpha-Cluster-Modell anscheinend ebenfalls in einem gewissen, bislang nicht aufgelösten Widerspruch zur
quantentheoretisch fundamentalen Unschärferelation von Werner Heisenberg. -
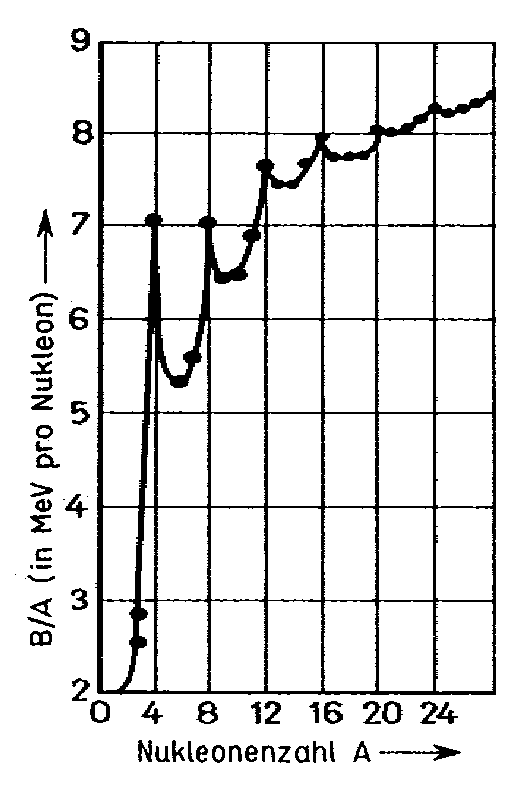
Immerhin liefert das Kernmechanische Modell gleichermaßen eine gute (und womöglich bessere) Erklärung für die jeweils bei Kernen mit einer durch vier teilbaren Massenzahl beobachteten Bindungsenergie-Maxima: Durch die z. T. dipolartig wirkende starke Kernkraft zwischen den Nukleonen – auch die elektrische Ladung spielt noch eine Rolle – bilden sich hier Kernringe, bevorzugt aus jeweils (4), 6, 8 (oder 10) Nukleonen, welche dann (ab 5 Nukleonen) auch als “Kettenglieder” quasi ineinander greifen können. Für He-4 gilt das aber eben nun gerade nicht! Dennoch ergeben sich völlig zwanglos die
in ihrer Bindungsenergie besonders ausgezeichneten Isotope He-4, Be-8, C-12 (2x 6), O-16 (2x 8), Ne-20 (6 + 8 + 6), Mg-24 (3x 8), Si-28 (6 + 8 + 8 + 6).6
Eine Besonderheit des Kernmechanischen Modells ist die in bestimmten Fällen beobachtbare sogenannte Selbstähnlichkeit der chemisch-atomaren Bindungsstrukturen mit den – hier – ganz realen Kernstrukturen. So finden sich etwa die 5er Kernringe des Elementes Bor wieder in den typischen Ikosaeder-Kristallen oder die 6er Kernringe von Kohlenstoff in dessen aromatischen Verbindungen.
Bei Schwefel-32 mit vier 8er-Kernringen bilden nach einem ersten Erklärungsmodell sowohl die Protonen von zwei parallelen
Kernringen, als auch die acht Atome einer S-8-Molekel jeweils eine räumliche Anordnung zweier gegeneinander versetzter Vierecke in zwei Ebenen zu einem “gestauchten” Achteck.
Ganz ähnlich liegen die Verhältnisse auch “beim Zink-64, wo sich die acht Kernringe zwangsläufig zu einem langgezogenen Rhombus ordnen,
der dann bei der Dehnung eines stabförmigen Zink-Einkristalls in Gestalt der charakteristischen Gleitebenen wiederum deutlich zu Tage tritt.” 7
Die durch die Kernmechanik beschriebenen Modellstrukturen umfassen dann aber - im Gegensatz zum
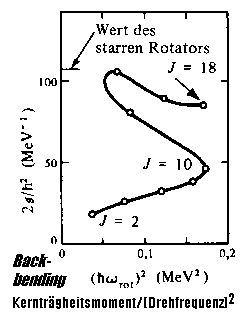
naiv-abstrakten Alpha-Cluster-Modell - weiterhin auch noch die mittel-/schweren und superschweren Kerne und erklären z. B. den “Backbending-Effekt”, d. h. die plötzliche Zunahme des Trägheitsmoments etwa beim Erbium, nun rein mechanisch dadurch, daß hier eine längere geschlossene und zusammengerollte, aus vielen einzelnen Kernringen bestehende Kette bei zunehmender Rotation durch die Fliehkraft plötzlich auseinandergezogen wird (4, s. o., S. 4).
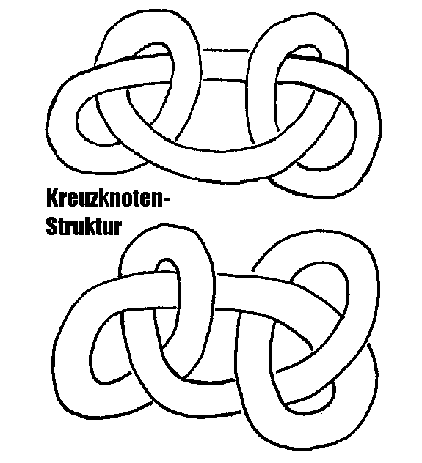
Bei längerer Kette wird dieser Effekt erst durch einen und dann beim Blei durch zwei stabilisierende Knoten(-umschlingungen) in der Kette verhindert, wodurch dort letztlich so etwas wie eine doppelt geflochtene feste Kranzstruktur (oder ein Ring zweiter Ordnung) entsteht. Genauso können die charakteristischen Eigenschaften etwa von Uran, insbesondere was die Spaltbarkeit anbelangt, z. B. direkt aus seiner Kreuzknoten-Struktur abgeleitet werden (4, s. Abb. rechts).
Des weiteren hat das Kernmechanische Modell bereits 1997 - jeweils mehr als ein Jahr vor der tatsächlichen Entdeckung - sowohl die Notwendigkeit einer “Neutrinomasse”, als auch die bei sehr weit entfernten
Galaxien beobachtete beschleunigte Expansion des Universums (lt. Science die wissenschaftliche Entdeckung des Jahres 1998) postuliert: “...durch den “Neutrinowind”... hängt es allein vom kosmologischen
Maßstab ab, ob dann innerhalb von Galaxien nun Anziehung, d. h. (großräumig nicht konstante) Gravitation oder darüberhinaus zunehmende Abstoßung und somit wachsende Rotverschiebung (Hubble-Fluchtgeschwindigkeit) auftritt.” 8
Dennoch sind beim zitierten Kernmechanischen Modell jedoch Widersprüche zu den geltenden Naturgesetzen, insbesondere gegenüber der Unschärferelation der
Quantenphysik, aber auch innerhalb des Modells unübersehbar: Etwa, was die jeweils angegebenen Kernstrukturen anbelangt oder auch die Berechnung der Dipolmomente, z. B. unter der etwas gewagt
erscheinenden Prämisse, daß Protonen (verschiedener Kernringe) jeweils paarweise mit parallelem Spin zusammenkoppeln sollen, damit am Ende nur das Ergebnis “stimmt”!- Das aber erinnert eher an mathematische Taschenspielertricks, wie sie – vollkommen zu Recht – etwa auch der Stringtheorie vorgeworfen werden!
Aller berechtigten Skepsis zum Trotz gibt es hier aber dennoch eine nicht nur rein mathematische, sondern
physikalisch realistische Lösung, wenn man nun annimmt, daß alle im Atom vorkommenden Elementarteilchen wie Protonen, Neutronen, Elektronen, Photonen und ihre Antiteilchen sich auf genau definierten
Bahnen, bei Abwesenheit sonstiger Felder: auf - durch Neutrinos und Teilchenspin bewirkten - Kreisbahnen, jeweils um ihren eigenen (zeitlich gemittelten, in Wirklichkeit aber leeren) virtuellen
Schwerpunkt bewegen.
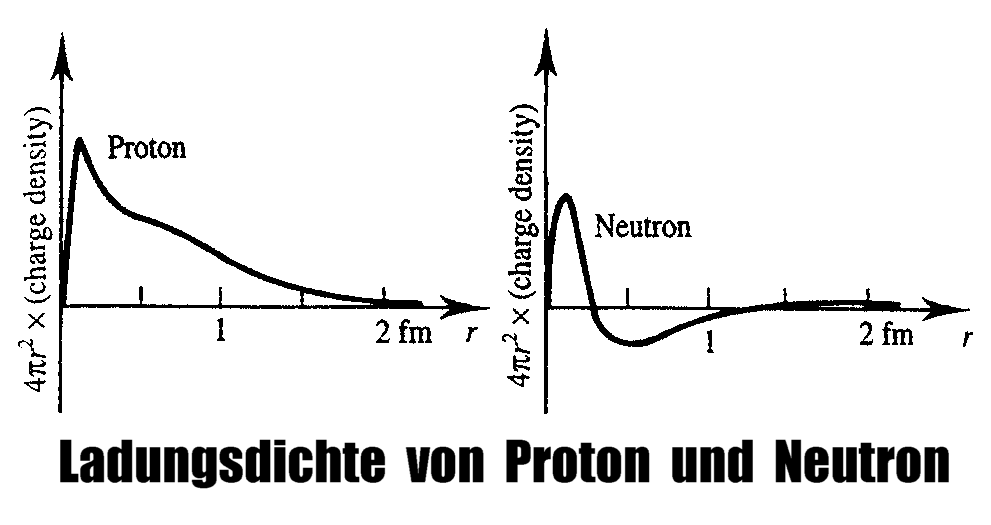
>> Die starke Kernkraft resultiert dann hauptsächlich aus der besonderen, am äußeren Rand negativen und damit zu der der Protonen komplementären Ladungsdichte der Neutronen, wobei in der Folge nun auch gebundene Zustände möglich sind.
Alsdann sind die jeweiligen angeregten Energieniveaus eines bestimmten Atomkerns direkt aus der Ladungsdichteverteilung der einzelnen
Nukleonen, sowie über die Kerngeometrie und die daraus abgeleiteten gegenseitigen Nukleonen-Abstände zu berechnen.
Ferner ist der Kernspin eines Nuklids im Grundzustand oder in einem angeregten Zustand nun außerdem aus Symmetrieabweichungen der
Nukleonen eines Kernrings oder mehrerer Kernringe zueinander abzuleiten,- wobei fehlende oder zuviel vorhandene Nukleon jeweils mit I = ½ und komplementäre Nukleonen, also Proton und Neutron (statt
Proton – Proton oder Neutron – Neutron), mit I = 1 bewertet werden.
Es scheint notwendig, hier gleich noch die Bemerkung anzufügen, daß der zuvor konstatierte (od. konstruierte) Widerspruch des alten
Kernmechanischen Modells zu den Naturgesetzen nur ein scheinbarer ist; denn natürlich gibt es grundsätzlich nur von Menschen gemachte (“Natur”-)Gesetze.- Dabei ist eigentlich schon die Suggestivfrage:
“Klassische oder Quantenphysik?” nicht nur irreführend, sondern sogar falsch, da eine solche Alternative in Bezug auf die Vorgänge im Atominneren überhaupt nicht existiert, genauso wenig wie etwa Farbe
als reales Beschreibungskriterium für Elementarteilchen. Da es sich bei den Elementarteilchen, um die es hier vor allem geht, nachgewiesenermaßen um Quanten handelt, kann die Frage demnach nur lauten: “Reicht
die fast hundert Jahre alte Quantenphysik, welche u. a. eine konkrete mechanische Rolle des Teilchenspins negiert, zur Beschreibung der elementaren Vorgänge heute noch immer aus, oder ist der
Millenniumswechsel nicht doch der richtige Zeitpunkt für eine bessere neue?!” -
Für den, der hören wollte, war die Botschaft aus - sehr kenntnisreich und mit viel
Engagement durchgeführten - Experimenten von Alan D. Krisch und seiner US-Forschungsgruppe mit polarisierten Protonen, die bei sehr hohen Energien aneinander gestreut wurden 9, spätestens seit 1987 eigentlich schon unüberhörbar:
“Unser zweites Ergebnis bringt jedoch die QCD (Quantenchromodynamik - die von Murray Gell-Mann entwickelte Quark-Theorie der Teilchenstreuung) in ernsthafte Schwierigkeiten. Wir stellten fest, daß bei
Energien über 8 GeV der Wirkungsquerschnitt schneller abfällt, wenn die Spins der Protonen antiparallel sind, als wenn sie parallel sind. Die Chance für einen Stoß mit großem Energieübertrag ist demnach
aus irgendeinem Grunde größer, wenn die Spins der Protonen parallel sind. Bei 13 GeV ist der Wirkungsquerschnitt... dann viermal größer, als wenn sie antiparallel sind. Wir wissen zwar nicht genau, was
dieses völlig unerwartete Verhalten verursacht – ganz sicherlich aber ist dieses Ergebnis keine gute Nachricht für die QCD.” (bdw)
Proton-Proton-Stöße mit großem Energieübertrag fanden demnach dann statt, wenn Strahl und Target in dieselbe Richtung polarisiert
waren. Bei Entgegengesetzter Polarisierung, wenn also mechanisch - bildlich gesprochen - ein linksherum rotierendes auf ein rechtsherum rotierendes Proton traf, “schienen die Protonen häufig praktisch
ohne Wechselwirkung einander zu durchdringen.”
War dies allein schon schlimm genug für die Quantenchromodynamik, die noch immer allgemein akzeptierte Theorie der starken
Wechselwirkung, so kam es bei weiteren Experimenten mit einem unpolarisierten Protonenstrahl, der auf ein polarisiertes Target gerichtet wurde, dann doch noch schlimmer: “Bei Stößen mit einer Energie von
28 GeV war die Zahl der nach links gestreuten Protonen bei großen Streuwinkeln um etwa 60% größer als die Zahl der nach rechts gestreuten!”-
Im übrigen, so bemängelte der Physikprofessor der Universität von Michigan, “hat die Theorie... nur
wenige Vorhersagen gemacht, die experimentell nachgeprüft werden konnten. Die QCD ist zwar eine sehr flexible Theorie und konnte den meisten Streudaten im nachhinein leicht angepaßt werden; ich lasse
mich jedoch weniger durch die Anpassungsfähigkeit einer Theorie beeindrucken als durch ihre Voraussagekraft.” Womöglich hat aber die 2000 gerade neun Jahre alt gewordene Kernmechanik (anfangs auch: “Kernphysikalische Chemie”)
hier ebenfalls doch noch etwas mehr zu bieten...
Einige Beispiele für das Realistische Kernmechanische Modell sind in der Zeichnung dargestellt und z. T. zusätzlich als Modelle verfügbar. Es zeigen:
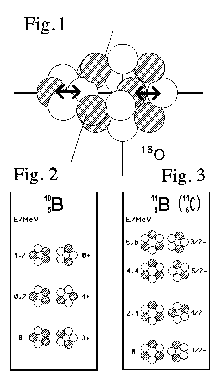
Fig. 1 das aus zwei Kernringen mit je acht Nukleonen bestehende O-16-Nuklid schematisch in einer perspektivisch realistischen Darstellung
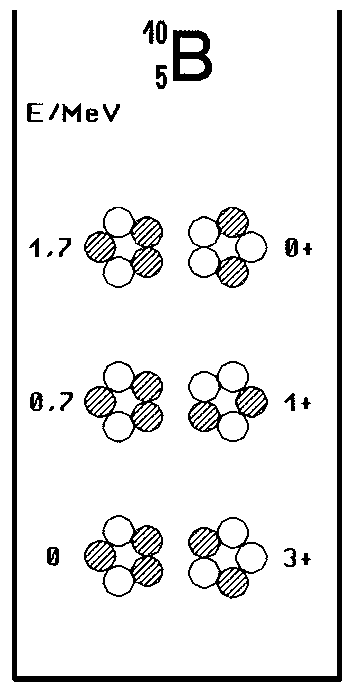
Fig. 2 das Termschema von B-10 in einer schematisch realistischen 2-D-Darstellung der jeweiligen Anordnung der Kernringe im
Grundzustand und in angeregten Zuständen
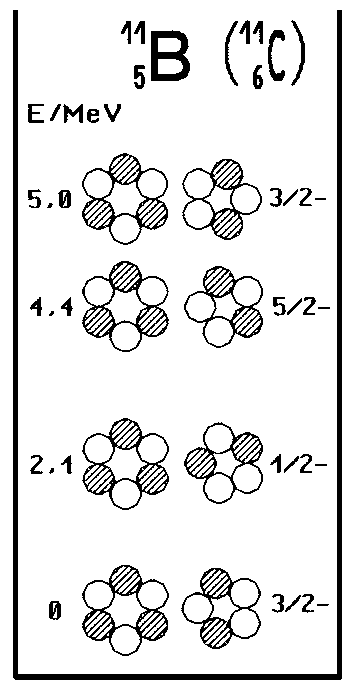
Fig. 3 das Termschema von B-11 in gleicher Darstellung wie Fig. 2
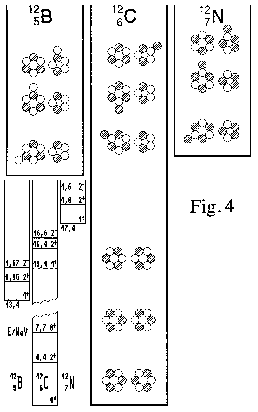
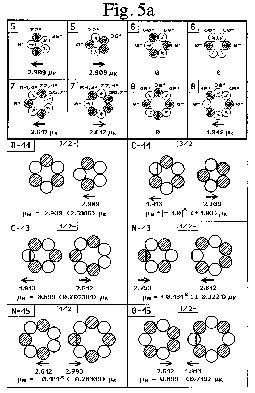
Fig. 4 das Termschema der A =12 Kerne B-12, C-12 und N-12 in gleicher Darstellung wie Fig. 2 + 3, mit zugehörigem Niveauschema links
unten
Fig. 5 eine systematische Aufstellung der wichtigsten Kernringe, schematisch, mit jeweils eingezeichneter Ausrichtung der
Dipolmoment-Vektoren und danach in einer schematisch realistischen 2-D- Darstellung: eine Übersicht wichtiger Nuklide von B-11 bis Mg-25 mit der jeweiligen Anordnung der Kernringe im Grundzustand
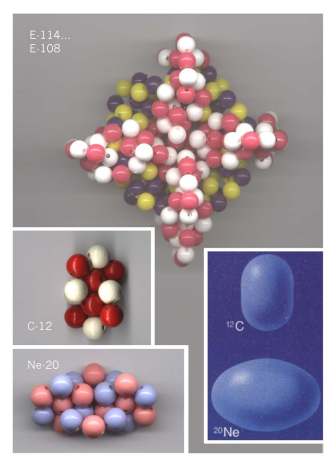
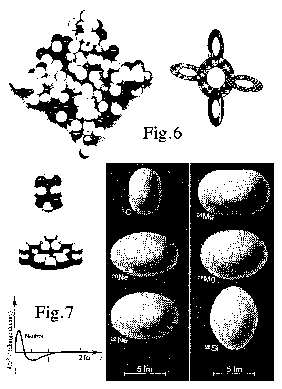
Fig. 6 , oben links, ein Perlenmodell der komplexen Nuklidstruktur von E-114 bis E-108 in einer vergröberten Umrißzeichnung und oben
rechts, das zugehörige Schema mit einem zentralen Kernring zweiter Ordnung und vier einzufügenden kleineren Kernringen; darunter dann jeweils eine Gegenüberstellung der Nuklide von C-12 und Ne-20, als
Darstellung im Perlenmodell, links, und aus Messungen ermittelte Kernformen1, rechts.
Fig. 7 zeigt schließlich eine Kurve der Ladungsdichteverteilung, wie sie für das Neutron ermittelt wurde10.
Wie man aus der Fig. 1 ersieht, sind beim O-16-Nuklid – und nicht nur dort – die Protonen und Neutronen (so weit als möglich) immer alternierend
angeordnet. Dies ergibt sich schon aus der Wirkungsweise der starken Kernkraft, welche demnach hauptsächlich aus der besonderen, am äußeren Rand negativen - und damit zu der der Protonen komplementären -
Ladungsdichte der Neutronen resultiert.
Die bislang vor allem aus der Streuung zwischen Protonen und Neutronen, Protonen und Protonen, sowie Neutronen und Neutronen
konstatierte Ladungsunabhängigkeit der Kernkräfte, insbesondere nach dem rechnerischen Berücksichtigen der üblichen Austauschterme für identische Fermionen und der Coulomb-Wirkung, erweist sich also als
Fehlschluß: “Die zwischen beiden Teilchen wirkende Kernkraft würde sich nicht ändern, wenn man die Coulomb-Wechselwirkung ausschalten könnte;”- gerade das aber ist grundsätzlich nicht möglich (was wieder
einmal mehr zeigt, daß man mit falschen Voraussetzungen alles beweisen kann)!
Doch zurück zu den beiden aus jeweils acht Nukleonen bestehenden Kernringen von O-16. Zu der ungestörten alternierenden Anordnung der
Nukleonen der einzelnen Kernringe kommt sodann noch die in der Fig. 1 mit Pfeilen symbolisierte energetisch günstige doppelte Kopplung zwischen je einem Proton des einen Ringes und einem Neutron des
anderen. Ein weiterer Grund für die auch als “magisch” bezeichnete Stabilität und Kugelform des O-16-Nuklids liegt womöglich in einer dritten – nicht eingezeichneten – inneren Kopplung zwischen den
beiden erwähnten Nukleonenpaaren.
Besonders interessant und unerwartet ist nun der Grundzustand von C-12 (Fig. 4, ganz unten), wo sich eben gerade nicht zwei Neutronen
innen befinden, sondern vielmehr zwei Protonen,- was an der kurzen Reichweite der Coulomb-Abstoßung der Neutronen liegt: Da die Ringkonfiguration beider Li-6-Kernringe ansonsten festliegt, stellen sich
diese in der Drehung dann so ein, daß sich möglichst kein Neutron im Ringinneren des anderen Kernringes und damit in Kontakt zu dessen drei Neutronen befindet.
Selbst wenn die (bei der Bindungsenergie negativ zu Buche schlagende) Abstoßungsenergie zweier Protonen in der Mitte des Nuklids noch
größer ist, als die der Neutronen an gleicher Stelle, so ist sie doch auch in der äußeren Position - anders als bei den Neutronen - immer noch sehr hoch. Entscheidend ist aber letztlich die (bei den
Neutronen hier größere) Energiedifferenz!
Aus dem gleichen Grund ergibt sich jetzt ebenso für B-10 eine zu früheren Annahmen komplementäre Grundkonfiguration, Fig. 2 unten,
woraus ein positives elektrisches Quadrupolmoment resultiert, das wie zuvor schon das magnetische Dipolmoment nunmehr exakt mit der Messung übereinstimmt. Beim ersten angeregten Zustand erscheint dann der in der Zeichnung rechte Kernring genau um eine “Raststellung” weitergedreht. Der Kernspin von I = 1 ergibt sich daraus, daß hier die Symmetrie zwischen linkem und rechtem Kernring durch genau ein abweichendes,
d. h. komplementäres Nukleon(enpaar) gestört ist. Beim Grundzustand handelt es sich jedoch um drei abweichende Nukleonen;- daher: I = 3.
Allgemein formuliert lautet die Kernspin-Regel dann so, daß der Kernspin eines Nuklids im Grundzustand oder in einem angeregten Zustand aus Symmetrieabweichungen der Nukleonen eines Kernrings oder mehrerer Kernringe zueinander abzuleiten sind, wobei nun fehlende oder zuviel vorhandene Nukleonen jeweils mit I = ½ und komplementäre Nukleonen, also Proton und Neutron (statt Proton – Proton oder Neutron – Neutron), jeweils mit I = 1 bewertet werden.
Das ist auch gut beim nebenstehenden Termschema von B-11 in der Fig. 3 zu erkennen, wo die jeweilige Ausrichtung des rechten
Kernrings als alleinige Variable für Energie und Kernspin bestimmend ist:
In beiden 3/2-Konfigurationen fallen dort die beiden symmetrischen Protonen aus der Rechnung heraus und es bleiben eben die
genannten 3/2 übrig oder beim ersten angeregten Zustand nur das Neutron ganz rechts (unten), also ½ usw. usw.. Des weiteren sind die jeweiligen angeregten Energieniveaus eines Atomkerns direkt aus der
Ladungsdichteverteilung der einzelnen Nukleonen, sowie über die Kerngeometrie und die daraus abgeleiteten gegenseitigen Nukleonen-Abstände zu berechnen.
Besonders leicht nachprüfbar sind die Kernspinzahlen übrigens ebenfalls noch bei Be-10 und C-10 (nicht gezeichnet), die in ihrem Aufbau
ansonsten B-10 entsprechen, mit jeweils I = 0 im Grundzustand und I = 2 in zwei angeregten Zuständen. Ansonsten ist die Ermittlung der richtigen Konfiguration, bzw. die richtige Zuordnung und Bewertung
nicht immer ganz einfach, wie man am Termschema der Kerne B-12, C-12 und N-12, Fig. 4, ersieht: Da ein He-6-Kernring offenbar weniger stabil oder gebunden ist als ein He-5-Ring, basieren B-12 und die
höheren Niveaus von C-12 offenbar auf der stabilen Grundkonfiguration von B-11. Dort kommt dann lediglich noch ein sehr lose gebundenes Nukleon hinzu, was man schon an den vergleichsweise kleinen
Niveauunterschieden erkennen kann. Noch geringer, aber ebenfalls sichtbar sind hier schließlich die Einflüsse der abweichenden Potentialverteilung bei Protonen und Neutronen.
Bei der Berechnung der magnetischen Dipolmomente kann man nun zunächst von den in der Fig. 5a oben aufgeführten einzelnen Kernringen
ausgehen, wo sich dann wie im Folgenden eingezeichnet durch vektorielle Addition die darunter aufgeführten Gesamtmomente für den jeweiligen Kern ergeben.
Das Dipolmoment des B-11-Nuklids entspricht dabei annähernd dem des He-5-Kernrings, da es hier offenbar im Gegensatz zu C-11 keine
weiteren bedeutenden Einflüsse gibt. Dort allerdings koppelt ein Proton (schwarz markiert) nun anscheinend innen - nicht ganz zentral - an ein Neutron des Li-6-Kernrings (durch senkrechten Balken
markiert), dessen Dipolmoment deshalb - weitgehend - eliminiert wird. Ein wichtiger Unterschied zwischen den beiden Kernen bei der Frage der Nukleonenankopplung besteht womöglich in dem
vergleichsweise größeren Durchmesser der Neutronen, der im ersten Fall bei B-11 eine solche dann aus geometrischen Gründen verhindern könnte. Wahrscheinlicher ist aber eine andere Erklärung, wozu es noch
einiger Vorbemerkungen bedarf:
In diesem Zusammenhang ist es sinnvoll, als erstes etwas genauer auf die mit den unterschiedlichen Konfigurationen verknüpften
Energieniveaus im Termschema von B-11 (und C-11) in Fig. 3 einzugehen. Bei einem kritischen Vergleich mit den unteren drei Niveaus von C-12 in Fig. 4 verwundert es zunächst, daß im ersten Fall bei B-11
und dem eng damit korrelierten Spiegelkern C-11 so gar nichts von dem bei C-12 festgestellten größeren Einfluß der jeweiligen Kernring-Neutronen zu spüren ist.
Näheres Hinsehen offenbart dann aber doch durchaus große Unterschiede zwischen den beiden Fällen: Während bei den Kernringen von C-12
die Ladungsschwerpunkte von Protonen und Neutronen jeweils (mit dem Kreismittelpunkt) zusammenfallen, weisen die He-5- bzw. Li-5-Kernringe eine große “Ladungsunwucht” auf, wo die niedrigste Energie – im
Termschema deutlich ablesbar – für das gleichnamige Nukleonenpaar immer ganz außen zu finden ist.
Daß das so ist, liegt aber vor allem noch in einem zweiten wichtigen Umstand begründet: Schon ein relativ gering erscheinender
Unterschied des Kernringdurchmessers von hier fünf statt sechs Nukleonen kann angesichts ihrer Ladungsdichteverteilung, insbesondere der der Neutronen – vergl. Fig. 7 –, darüber entscheiden, ob man es
bei den gegenseitigen Wechselwirkungen noch mit “linearer” oder schon mit “nichtlinearer” Nukleonenphysik zu tun hat! Hinzu kommt noch die gänzlich unbestrittene Tatsache, daß eben diese
Nukleonen keine kleinen harten Billardkugeln sind. Sie sind vielmehr weitgehend leer und bestehen eigentlich nur aus einem rotierenden “Nichts”, d. h. aus schwer faßbaren Substrukturen (“Quarks”) mit
definiertem Spin.
Dabei ist es dann wie schon beschrieben durchaus möglich, daß sich Nukleonen gegenseitig z. T. ungestört durchdringen,- wenn z. B.
deren Spin nicht parallel, sondern antiparallel zueinander ausgerichtet ist. Dergleichen könnte alsdann auch bei Protonen und Neutronen zweier entsprechend “synchronisierter” Kernringe passieren und
sollte sich dann etwa in der vektoriellen Orientierung der Dipolmomente offenbaren!-
Wahrscheinlich ist dies bei mindestens zwei der in der Fig. 5a dargestellten Nuklide, nämlich C-13 und N-13, tatsächlich der Fall,
weshalb hier nun der Vektor des jeweils rechten Kernrings in die entgegengesetzte Richtung weist und sich ebenso das Vorzeichen insgesamt umkehrt, d. h. bei C-13, trotz der mehrheitlich vorhandenen
Neutronen, dennoch positiv ist und bei N-13 zumindest teilweise negativ. Möglich wäre weiterhin auch, daß etwa bei B-11 und C-11 der rechte 5er-Ring, statt wie in der Zeichnung “auf Lücke” angeordnet,
nun ein Proton des anderen Kernrings – mehr oder weniger – ganz umschließt;- mit den entsprechenden Auswirkungen.
Zweierlei wäre damit “gewonnen”: Zum einen läge der Vektor des markierten Neutrons von C-11 jetzt auf einer Achse in direktem Kontakt
mit dem ebenfalls markierten Proton des rechten Kernringes, wodurch wie schon gesagt dessen Dipolmoment eliminiert wird. Zum anderen stünden sich dann beim Spiegelkern B-11 an gleicher Stelle lediglich
zwei (nicht reagierende) Neutronen gegenüber.
Ansonsten ist zur Feinkorrektur der Dipolmomentberechnung, z. B. beim Be-7 Kernring von N-13, zusätzlich ebenfalls noch dessen
Deformation mit einzukalkulieren (wobei sich eine Stauchung hier verkleinernd auf das Ringmoment auswirkt), u. U. aber ebenso, daß auch das “eliminierte Dipolmoment” eines Nukleons wohl niemals ganz
genau auf Null reduziert sein wird!-
Praktisch noch nicht zu berechnen ist deshalb der aus einem Be-8- und einem darauf aufgereihten Li-6-Kernring bestehende Kern von N-14
(nicht gezeichnet). Umgekehrt ist es aber sehr wohl möglich, im Gegenzug daraus zu lernen: Etwa, daß das innere Neutron nur sehr geringen “Kontakt” hat zum gegenüberliegenden Proton des deformierten
Be-8-Ringes, woraus dann letzten Endes die hier gemessenen 0,40361 Kernmagnetonen resultieren (nicht hingegen aus der Deformation des symmetrischen und neutralen Be-8-Rings). Im übrigen stimmt auch der
Kernspin I = 1 mit dem einen im Inneren vorhandenen komplementären Nukleonenpaar genau überein.- Anzumerken bleibt nur noch, daß der Isoton-Kern C-14 anders, nämlich aus zwei Li-7-Kernringen
zusammengesetzt ist.
Bei N-15 (und O-15) ist es hingegen so, daß laut Fig. 5a der rechte Be-8-Kernring, durch starke elektrostatische Abstoßung nach außen
getrieben, - nur hier - jeweils allein innen an die beiden Neutronen des Li-7-Kernrings (bzw. bei O-15 an die beiden Protonen des Be-7-Kernrings) ankoppelt; Dipolmomentberechnung gleichfalls in der Fig.
5a.
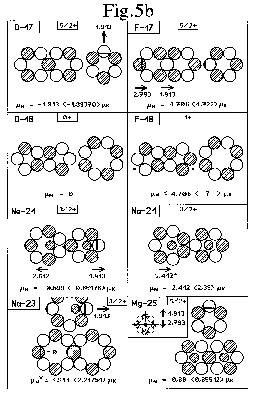
Bei O-17 und F-17, Fig. 5b, kommt erstmals eine besondere Kernstruktur zum Tragen: quasi eine “liegende 8” aus zwei mit einander
verschmolzenen Li-6-Kernringen, die sodann jedoch ein fehlendes Proton oder Neutron “gemeinsam besitzen”, was übrigens im folgenden Fall bei F-19 und Ne-19 (nicht gezeichnet) sowohl am Kernspin als auch am Dipolmoment unmittelbar abzulesen ist. Der dort vorhandene Be-8-Kernring hat dabei, außer einer stabilisierenden Funktion, keinerlei Einfluß auf das Dipolmoment der beiden Nuklide, welches im übrigen ausschließlich auf das eine fehlende Nukleon zurückgeht.
O-17 und F-17 verfügen an Stelle des Be-8-Kernringes jedoch über einen Li-6-Kernring, welcher sehr wohl bestimmenden Einfluß auf die
Kerneigenschaften hat. Das beginnt mit der jeweils durch fünf seiner Nukleonen – quer zur Längsachse – gestörten Symmetrie, also: I = 5/2 und setzt sich fort beim in der gleichen Richtung wirkenden
Dipolmoment und folglich auch einem negativen Quadrupolmoment.
Dabei wird in der besonderen Konstellation von O-17 offenbar das zentrale Dipolmoment unterdrückt, während sich bei F-17 die Momente
beider betroffener Nukleonen anscheinend addieren. Im letzten Fall ist es dann aber wahrscheinlicher, insbesondere falls sich nun das Quadrupolmoment als positiv erweisen sollte, daß der Li-6-Ring
gegenüber O-17 eine um 30 bzw. 90° gedrehte Position einnimmt. Am Kernspin von F-17 mit I = 5/2 ändert sich dabei überhaupt nichts!
O-18 hat zwar den Kernspin Null wie ebenso schon der magische Kern O-16, ist aber dennoch von ganz besonderer Bedeutung, da hier der Nuklidaufbau, und in der Folge die Ausrichtung der Protonen deutlich von den beiden vorhergehenden Sauerstoffisotopen abweicht. Das sollte sich in bestimmten Grenzfällen auch bei den chemischen Bindungen bemerkbar machen.
Ein solcher Grenzfall ist offenbar die Supraleitung und in der Tat hat der Physiker Alex Müller am 1. 7. 1997 bei der Tagung der
Nobelpreisträger in Lindau am Bodensee mitgeteilt, daß sich bei bestimmten Verbindungen die Eigenschaft supraleitend zu sein beim Austausch von O-16 gegen O-18 drastisch geändert habe!-
Falls übrigens die - nicht nur - vom Kernspin I = 1 suggerierte Darstellung der Kernringe von F-18 zutrifft, sollte das zugehörige
Dipolmoment, das sich gleichermaßen aus den beiden komplementären Nukleonen oder Kernringen ergibt, beachtliche 4,706 Kernmagnetonen betragen (oder etwas weniger)!- Beim Kernspin gibt es ansonsten aber noch weitere Übereinstimmung: Wie beim ganz ähnlich strukturierten B-10 findet man hier die Quantenzahlen 1, 3 und 0;- wenn auch in leicht veränderter Reihenfolge.
Daß bei einem Kernring mit gleichmäßiger Ladungsverteilung (siehe Li-6-Ring bei C-12) die energetisch günstigste Protonenposition zunächst einmal
innen ist, zeigt sich auch am folgenden Beispiel: In der Zeichnung der beiden Nuklide Ne-21 und Na-21 sind vom zentralen Be-8-Ring der besseren Übersichtlichkeit wegen nur die zwei jeweils auf der
Längsachse - auch hier innen - befindlichen Protonen (in verkleinerter Form) angedeutet, Fig. 5b.
Im ersten Fall, bei Ne-21, gibt es dann die Ankopplung eines dieser Protonen an ein – ebenfalls auf der Längsachse liegendes – äußeres
Neutron, wodurch dessen Dipolmoment wiederum eliminiert wird. Im zweiten Fall, bei Na-21, liegt stattdessen dort aber ein Proton. Hier gibt es also keine Ankopplung, sondern lediglich eine geringfügige Deformation beim anderen Kernring (Be-7), was für diesen zum Abzug von 0,2 MK führt.
Nachdem für das Nuklid Mg-24, das nach Fig. 6 die Form eines abgeplatteten Zylinders hat, alle verfügbaren Daten für eine
Grundstruktur aus drei Be-8-Kernringen sprechen, wie u. a. auch die Reaktionsgleichung: O-16 + Ne-20 = Mg-24 + C-12, ist offenbar Mg-25 schon aus vier Kernringen zusammengesetzt. Bei Na-23 scheint hingegen der Kernspin von I = 3/2 eine 3-Ring-Konfiguration einfach nicht zuzulassen, zumal in diesem Fall gerade immer nur ein ungepaartes Nukleon übrig bleibt.-
Wenn nun aber zwei 8er-Ringe zu einer 17-Nukleonenstruktur in Form einer liegenden Acht verschmolzen werden, Fig. 5b, wobei beide
vormaligen 8er-Ringe nunmehr analog zu O-17 oder F-19 wiederum ein zentrales Proton - nur einmal - gemeinsam besitzen, gibt es sodann jedoch sehr wohl eine Lösung, wo nicht nur der Kernspin,
sondern auch das Dipolmoment richtig herauskommen. Stimmen tut die Rechnung allerdings nur, wenn der dritte. mittlere Be-8-Ring asymmetrisch mit einem Neutron einseitig an ein äußeres Proton und mit dem
gegenüberliegenden Neutron innen an das zuvor erwähnte zentrale Proton der besagten 17-Nukleonenstruktur ankoppelt.
Genau dies ist zugleich aber auch der energetisch niedrigste Zustand,- also gerade der gesuchte Grundzustand, wo nun in der
Dipolmomentberechnung das äußere Proton durch das von innen angekoppelte Neutron nach der schon oben praktizierten Regel zu Null wird, während sich das zentrale Proton insgesamt nur wenig beeinflußt
zeigt. Gleichwohl bewirkt es aber, indem es von innen an ein Neutron des “beweglichen” mittleren Ringes ankoppelt , daß dessen Moment folglich von dem zuvor den Wert Null aufweisenden Dipolmoment des
Be-8-Kernringes abgezogen werden muß.
Gut nachvollziehbar sind Kernspin und Dipolmoment insbesondere aber beim mit 2,62 Jahren bemerkenswert langlebigen Na-22-Isotop.
Dieses setzt sich nämlich nun gleich aus zwei ineinander verschränkten komplementären A=11-Grundkonfigurationen zusammen, wobei sich der Kernspin I = 3 direkt aus der antisymmetrischen Anordnung der
axialen Nukleonen, P-N-N-P-P-N, ergibt.
Für Mg-25 bildet dann die schon bekannte, leicht von O-17 abweichende F-19-Kernstruktur wieder die Grundlage, wobei in den zentralen
Be-8-Ring diesmal noch ein Li-6-Ring eingefügt ist.-
Nach all den obigen Darlegungen scheint es nun allerdings an der Zeit, auch einmal darauf hinzuweisen, daß es zwar im einzelnen stets
gute Gründe für die jeweiligen Einschätzungen und vorgestellten Lösungen gibt, daß aber ebenso schon kleine Zuordnungsfehler, etwa in Bezug auf den tatsächlichen Grundzustand, weitere Folgefehler
nach sich ziehen können: Wenn also etwa der Grundzustand falsch angegeben wird, müssen natürlich auch die darauf fußenden Berechnungen – insbesondere für gleich strukturierte Spiegelkerne – dann
zwangsläufig ebenfalls falsch sein!
Soviel zum grundsätzlich nach wissenschaftlichen Regeln an Hand konkreter nachprüfbarer Voraussagen(!) – im Gegensatz zu manch anderen Modellen – auch f a l s i f i z i e r b a r e n
Realistischen Kernmechanischen Modell. Neben den vielen– vor allem auf dem Gebiet der Schwerionenforschung und in der Astronomie – bereits eingetroffenen Voraussagen ,soll hier nun außer beim Dipolmoment von F-18, Fig. 5b, gleich noch eine zweite gewagt werden, die sich an die obige anschließt, vom Atomgewicht her aber noch davor liegt:
Lithium 7 und Beryllium-7 sollten, abgesehen vom Vorzeichen, ebenfalls jeweils genau das gleiche Dipolmoment aufweisen, da auch ihre Kernstruktur gleich ist. In beiden Fällen wird nämlich der 5er-Kernring, einmal He-5 und einmal Li-5, durch einen axialen Deuterium-Kern stabilisiert, dessen Dipolmoment annähernd senkrecht zu dem des Kernrings steht: Nur annähernd übrigens
auf Grund der eher weichen Nukleonen-Konsistenz, welche schon bei den ersten beschriebenen Nukliden B-11...N-13, s. o., offenbar zur Vorzeichenumkehrung bestimmter Parameter geführt hat.-
Besonders instabil, da nur aus zwei gegeneinander gedrückten Kleinringen, H-3 und He-3, zusammengesetzt, ist auch der entsprechend
leicht teilbare und als bevorzugter Tritium-Spender dienende Li-6-Kern. In die gleiche Reihe der bei Kernprozessen leicht wieder zerfallenden Nuklide gehört ebenso Be-9, das allem Anschein nach
eigentlich ein “unvollständiger” C-12-Kern ist.- Daß das durch den halben Li-6-Ring bestimmte Dipolmoment nicht 0,88 MK ist, sondern etwas größer, liegt daran, daß auch der Winkel, den die beiden
Neutronen bezüglich der inneren Protonen einnehmen, nicht mehr wie in der Tafel von Fig. 6 gezeichnet 60° beträgt, sondern nunmehr fast ziemlich genau 65°.
Einige charakteristische Kernreaktionen wurden bereits im besonderen Kontext erwähnt. Man kann diese aber auch ganz gezielt
systematisch zur Überprüfung bestimmter fraglicher Kernstrukturen heranziehen, wobei natürlich ebenfalls der bestens bekannte Wirkungsquerschnitt für thermische Neutronen und dergleichen mit
einzubeziehen sind.
Das Realistische Kernmechanische Modell findet hier jedenfalls nun vielfältige Bestätigung, bzw. es konnten auf diese Weise ebenfalls in der Vergangenheit noch vorhandene Fehler und Irrtümer wirksam aufgespürt und beseitigt werden. Dank der jetzt über die konkreten Kernstrukturen gewonnenen Erkenntnisse ist es fortan auch nicht mehr nötig, auf so umstrittene Dogmen wie etwa Paritätserhaltung im allgemeinen und bei der starken Wechselwirkung im besonderen zurückzugreifen, um bestimmte Kernreaktionen zu erklären. Daß etwa F-19 durch Protonenbeschuß praktisch nicht in Ne-20 umgewandelt werden kann, wird nun unmittelbar einsichtig wie auch der entsprechende, naturgemäß gleichfalls erfolglose Versuch bei Na-23.
Für Mg-24 bleibt dann, nach dem Ausschluß aller alternativen Möglichkeiten, tatsächlich nur die etwas einsam in der Umgebung stehende 3x
Be-8-Ring-Konfiguration übrig, wobei hier für zwei Be-8-Kernringe eventuell auch eine quasi komplementäre “Sandwich-Anordnung” angenommen werden kann.
Bei Mg-26 (Al-26) kann hernach schon auf die “Sparlösung” von Mg-25 verzichtet werden, da es hier bereits für einen Be-8-Ring und drei
komplette Li-6-Ringe reicht, von denen einer bei Al-27 durch einen Li-7-Ring ersetzt wird; all dies offenbar kompatibel mit Kernspin, Dipolmoment usw. -
Noch einmal wird die “Mg-25-Sparlösung” dann bei Si-29 und P-31,
beide: I = ½, praktiziert. Das führt zur Strukturformel F-19 + 5 + 5 bzw. F-19 + 6 + 6, während S-32 danach, außer über den grundlegenden Be-8-Ring, wohl schon über vier Li-6-Ringe verfügt (Variante, s. o.: erweiterte Mg-24-Konfiguration 4x 8).- S-33, mit bereits einem (nun umgedrehten!) Li-7-Ring stattdessen, ähnelt dann – nicht nur beim Dipolmoment – ansonsten wieder einer “kleeblattartig” erweiterten Ne-21-Struktur. Das gleiche Dipolmoment, aber nun zwei Be-7- statt der Li-6- Kernringe, zeichnen anschließend das Ar-35-Nuklid aus.
Bei den folgenden “Dipolmoment-Zwillingen” S-35 und Ar-37 ist danach offenbar erstmals der zentrale Kernring um zwei Neutronen
erweitert, verbunden mit einer kleinen Winkeländerung des Li-7-Rings, aber ansonsten ohne grundlegenden Einfluß auf die von den Zentralring-Protonen bestimmte Symmetrie der beiden Kernring-Achsen. -
“Ideale” Verhältnisse, was die Kerngeometrie anbelangt, herrschen sodann erstmals wieder beim (sogar “doppelt-”)magischen Ca-40-Kern, der zu seinem zentralen B-10-Ring und der durch die Kernringprotonen vorgegebenen fünffachen Symmetrie nunmehr in idealer Weise ebenso gerade über fünf Li-6 Kernringe (mit genügend Freiraum!) verfügt.
Daß dies wohl so zutreffen mag, dafür sprechen etwa auch die Kerndaten von Ca-41 (und abgewandelt auch von Ca-43), welche demnach
hauptsächlich von einem (bzw. mehreren) – geometrisch genau richtig – deformierten Li-7-Kernring bestimmt werden. So gibt es also für alle Quantenzahlen, und seien sie auch noch so magisch, am Ende letztlich
doch eine überzeugende kernmechanische Erklärung.
Darüber hinaus finden sich die Kernformen, die durch das Realistische Kernmechanische Modell erzeugt werden können, z. B. über
Perlenmodelle, ebenfalls wiederum verblüffend realistisch in den durch kerntechnische Messungen bestimmten Kernformen wieder, Fig. 6 Mitte. Links dort eine - hier vergröberte -Abbildung des Perlenmodells
von C-12, rechts daneben die gemessene Form1.
Nebenbei gesagt, im neuen realistischen Modell, mit den jetzt innen angeordneten Protonen, stimmt nunmehr auch die
Ladungsdichteverteilung perfekt mit der Messung überein, wie ebenso bei O-16.- Darunter in der vergleichenden Abbildung ebenfalls noch Ne-20, das Nuklid “mit der Bauchbinde”, die dann bei Ne-22 in ein an
den Enden stärker gerundetes Ellipsoid übergeht, eine Entwicklung die sich bis zu Mg-24, “ein abgerundeter Zylinder”, weiter fortsetzt. Mg-26 ist dann abermals ein Ellipsoid. -
Am oberen Ende in der “Schwergewichtsklasse” der Elemente wurde schon darauf hingewiesen, daß die relativ stabile Modifikation des
Elements 114 -
sowie die folgenden Elemente der Zerfallskette bis zu Element 108 - aus einem zentralen Kernring mit mindestens 80 Nukleonen und vier in symmetrischer Anordnung (Fig. 6) dort aufgereihten Kernringen mit mindestens 48 Nukleonen besteht.
Weiterhin kann durch das Realistische Kernmechanische Modell darauf geschlossen werden, daß das mit relativ hohem Wirkungsquerschnitt herstellbare Element 118 sowie die folgenden Elemente der Zerfallskette aus einem zentralen doppelten Kernring mit mindestens 208 Nukleonen und einem weiteren damit verschränkten Kernring von mindestens 64 Nukleonen zusammengesetzt ist und / oder daß der kürzere Kernring danach aufgebrochen und weiter verkürzt wird.
Die besondere stabile, innen “offene”, Kranzstruktur von Blei wurde ja schon früher beschrieben, zumal sie nicht nur hervorragend mit
der erst durch Alpha-Teilchen möglichen symmetrischen Spaltung korrespondiert, sondern nunmehr auch mit dem hohen Wirkungsquerschnitt der neu gefundenen Kernverschmelzungsreaktion mittels Krypton-Ionen
zum neuen “Element-118”, usw.. Was ansonsten noch den erstaunlich hohen Wirkungsquerschnitt bestimmter Kernreaktionen, der z. B. beim Neutroneneinfang durch Bor den eigentlichen Kerndurchmesser bei
weitem übertreffen kann, anbelangt, wird dieser nun durch die jetzt gefundene Ladungsabhängigkeit der starken Kernkraft unmittelbar einsichtig.
Voraussetzung für dies alles ist allerdings zunächst einmal die Bereitschaft, sich von alten (und “bewährten”) Vorurteilen zu trennen, was sicher
ggf. auch durch Widersprüche zwischen Theorie und Experiment gefördert wird. Nur kann es erfahrungsgemäß zuweilen lange dauern, bis alle möglichen Modifikationen und “Verbesserungen” bei einer für
unverzichtbar gehaltenen Theorie nicht mehr helfen.
Anscheinend gab es bislang wirklich keine Alternative zur alten Quantenmechanik, wo es ja zunächst Bohr mit seinem sogenannten
Planetenmodell der Atome geschafft hatte, die Spektrallinien im Spektrum des Wasserstoffatoms durch auf bestimmten erlaubten Bahnen um das Atom kreisende Elektronen zu erklären. Dieses Modell wurde erst
viele Jahre später aufgegeben, nachdem es trotz aller Anstrengungen nicht gelungen war, damit das Spektrum von Helium zu berechnen und durch die zeitunabhängige Schrödingersche Wellenmechanik ersetzt, wo
es keine konkreten Elektronenbahnen mehr gab, sondern nur noch Aufenthaltswahrscheinlichkeiten.
Im neuen Realistischen Kernmechanischen Modell ist es hingegen so, daß alle im Atom vorkommenden Elementarteilchen wie Protonen, Neutronen, Elektronen und ihre Antiteilchen, ebenso auch Photonen sich auf genau definierten Bahnen, bei Abwesenheit sonstiger Felder: auf - durch Neutrinos und Teilchenspin bewirkten - Kreisbahnen, jeweils um ihren eigenen virtuellen (zeitlich gemittelten, in Wirklichkeit aber leeren) Schwerpunkt bewegen. Der ansonsten punktförmige Aufenthaltsort von Elektronen etwa erscheint also (wie beim “zeilenfreien”
Fernsehehen) verschmiert durch eine überlagerte Kreisbewegung.
Die Wirkungsweise kann durch ein Analogie-Beispiel erklärt werden: etwa mit einer frei im Raum rotierenden “Supertaschenlampe”, die einen extrem
starken Lichtkegel abstrahlt und sich durch den von den Photonen erzeugten Lichtdruck dann auf einer Kreisbahn durch den Raum bewegt. -
So weit, so gut. Doch nun wird das Modell quasi umgedreht und das rotierende Objekt sendet keine gerichteten Partikel mehr aus, sondern
empfängt nur noch welche, ebenfalls gerichtet. Die empfangenen Partikel, die jeweils einen kleinen Impuls übertragen, sind nun allerdings keine Photonen mehr, sondern Neutrinos, die ja nach den neuesten
Erkenntnissen (in Super-Kamiokande) ebenfalls eine, wenn auch nur sehr kleine “Masse” besitzen. Das Ergebnis aber ist in jedem Fall dasselbe, - im einfachsten Falle - eben eine Kreisbahn! Und wenn der
Teilchenspin stabil ist, ist auch die Kreisbahn stabil – wie bei den Elektronen im Atom.
*)
Daß kreisende Elektronen Strahlung abgeben müssen, gilt natürlich nur im Makrokosmos, aber eben nicht im Mikrokosmos. Zudem funktioniert die Strahlungsemission ja auch nur über Quanten, also Photonen, und nicht etwa kontinuierlich.
Die Elektronenbahnen im Atom bestimmen sich demnach im einzelnen dadurch, wieviel Photonen das jeweilige Elektron aufgenommen bzw. noch
nicht wieder abgegeben hat. Wenn es alle abgegeben hat, befindet es logischerweise in der untersten Bahn. Weiter gilt: Jede Bahn kann mit maximal zwei Elektronen besetzt sein, wobei die Kreisbahnen die
“s”-Bahnen sind. Wenn die innersten beiden besetzt sind, kommen auch exzentrische (elliptische) Bahnen hinzu, in deren Brennpunkt aber gar nicht (unbedingt) der Kern steht, dem sich die “p”- und
“d”-Elektronen vielmehr ebenso nur nähern können, bis sie von der inneren Elektronenhülle wieder nach außen hin abgelenkt werden.
Die ansonsten auftretenden Energiedifferenzen erklären sich u. a. von daher, daß es etwa im Beispiel Helium einen Unterschied macht, ob
das zweite, das sogenannte Leuchtelektron, parallel, im gleichen Drehsinn, oder antiparallel (entgegengesetzt) zum ersten, den Kern unten umlaufenden Elektron, oder gar quer dazu um den Kern kreist. Der
erste Fall ist der energetisch ungünstigste, weshalb nun kein Elektron aus einer anderen höheren Bahn hierher springt, sondern ausschließlich eines mit der gleichen Ausrichtung. Die logische Folge: das Singulett-Termsystem oder, im anderen Fall, die ebenfalls beobachteten Tripletts. Natürlich kann das zweite Elektron nur beim Singulett-System in den 1s-Grundzustand gelangen, wo sich nach dem Realistischen Kernmechanischen Modell dann
beide Elektronen in einer Bahn und jeweils in Opposition zueinander befinden. Zurück zu “Atomspektren, Quantensprünge und Photonen”
Wenn es im Termschema von Helium und den hier besonders übersichtlich erscheinenden Alkaliatomen Übergänge nicht auch in Gegenrichtung,
also etwa statt nur von 4f zu 3d ebenfalls von 4p zu 3d, geben würde, könnte man ja vermuten, daß auch die 2s- und 3s-Zustände zusätzlich zum 1s-Elektron dann noch ebenso mit zwei weiteren Elektronen besetzt sein könnten, was das insgesamt höhere Energieniveau der s-Terme im Vergleich zu dem der p-Terme (statt durch die geometrischen Bahnunterschiede) sicher auch erklären würde.
(In der Tat wirkt es in diesem Zusammenhang schon etwas verdächtig, wenn im Experiment von Lamb und Rutherford Atome erst durch
Elektronenbeschuß in den höheren 2s-Energiezustand gebracht werden und am Ende die Energie wieder an ein Wolframblech abgeben, indem sie dort Elektronen auslösen, die sie ja genauso gut bereits
mitgebracht haben könnten...)
Im Ansatz ganz ernst gemeint und – auch in anderem Zusammenhang – sehr nützlich ist hingegen das
folgende Erklärungsmodell für den bei Atomen und Molekülen beobachteten Para- oder Diamagnetismus. Es bedient sich ebenfalls eines bildhaften Vergleichs wie dem obigen mit den Taschenlampen, nur daß
diese jetzt durch Magnete ersetzt werden: Wenn sich also die Magnetachse wie bei einem die Erde umkreisenden Raumschiff immer in Flugrichtung orientiert ist, so durchläuft sie bei einem Umlauf alle
Winkelstellungen von 0° über 90°, 180°, 270° bis wiederum zu 0°. Statistisch ist das Ergebnis also folglich Null.
Wird jedoch die Bahn, etwa durch ein äußeres Magnetfeld, von einer Kreisbahn zu einer Ellipse verändert, gilt dies definitiv aber nicht
mehr, da sich dann ja das magnetische Teil(chen) unterschiedlich lange in kernnaher und in kernferner Position befindet!- Ein solches Modell des paramagnetischen Verhaltens erklärte ebenfalls gut den
Anstieg des Para- bzw. Ferromagnetismus bei der Annäherung der Atome in einem Gitterverband und dann den plötzlichen Abfall auf “Null” bei noch größerer Annäherung der untersuchten Atome.
Der paramagnetische Effekt wird allerdings dann völlig kompensiert (und nur ein kleiner, vom Bahndurchmesser abhängender
diamagnetischer Effekt bleibt übrig), wenn dieselbe elliptische Bahn von zwei Elektronen besetzt ist, etwa von einem freien Elektronenpaar.- Zwei Elektronen auf einer solchen Bahn können jedoch
ebenso Teil einer Elektronenpaarbindung sein, die auf diese Weise eine vollkommen mechanische Erklärung findet.
Aber auch die “s”-Bahn des Wasserstoffs z. B. taugt zu einer Paarbindung; wenn nämlich die Bahnen zweier Atome so miteinander
synchronisiert sind, daß sich – zumindest – immer ein Elektron gerade zwischen beiden Atomen befindet und das andere außen. Bereits nach einer früheren naiven Vorstellung sollten ja die gerichteten
Verbindungen etwa beim Kohlenstoff durch die Protonenanordnung im Kern bestimmt werden. Dies hat sich nun in der Tat bestätigt.
Auch beim Sauerstoff lassen sich die beiden gerichteten Bindungen auf diese Weise herleiten, wobei z. B. beim Wassermolekül die
eigentlichen 90° u. a. durch die Abstoßung der beiden Protonen auf 106° vergrößert werden. Auf der gegenüberliegenden Seite des Sauerstoffs befindet sich dann außerdem noch ein freies Elektronenpaar, auf
einer genau in der Symmetrieebene liegenden Bahn,– allerdings nur bei O-16 und O-17. Bei O-18 verläuft diese Bahn geneigt im Winkel von etwa 45°. Dies war offenbar die tiefere Ursache für die bei der
Supraleitung festgestellten deutlichen Unterschiede und sollte eigentlich ebenso einen – wenn auch kleinen – Einfluß auf den Bindungswinkel von H2O haben?!
Aus der konkreten Elektronenstruktur des Sauerstoffatoms wird nun gleichfalls deutlich, daß es bei der O2-Molekel
tatsächlich nur eine kovalente Einfachbindung gibt und daß die beiden ungepaarten Elektronen den Paramagnetismus bewirken, aber dennoch zur relativ festen Bindung beitragen. Weiterhin ist nun klar, daß
Ozon kein geschlossenes Ringmolekül bilden kann und daß der Bindungswinkel durch die Abstoßung der ungepaarten Elektronen auf 117° erhöht wird. Weil deren nicht ganz rechtwinklig zueinander
ausgerichteten Bahnen jedoch miteinander synchronisiert sein müssen, hat das in diesem Fall Diamagnetismus zur Folge.
Es ist leider nicht möglich, an dieser Stelle auf alle Besonderheiten des Kohlenstoffs einzugehen. Daß sich der vielfach beobachtete
und z. T. leicht abgewandelte Bindungswinkel von 120° direkt aus der Selbstähnlichkeit mit der Konfiguration der Kernprotonen ableitet, wurde indes schon erwähnt. Die Anordnung der Elektronen im
Benzolring und in den aromatischen Verbindungen ergibt sich nunmehr jedoch beim Realistischen Kernmechanischen Modell unmittelbar daraus, daß sich die Elektronen, hier paarweise, auf - durch Neutrinos und Teilchenspin bewirkten - Kreisbahnen um ihren eigenen (eigentlich leeren) virtuellen Schwerpunkt bewegen. Demnach gibt es sie also wirklich: die im Benzolring umlaufenden Ringelektronen(-paare) in der – oder parallel zur – Ringebene. -
Da nun grundsätzlich die bislang bestehende Spinproblematik rein mechanisch aufgelöst und erklärt werden konnte, bleibt jetzt
eigentlich nur noch die Frage nach den Welleneigenschaften von Teilchen,- insbesondere nach ihrer Interferenz. Wie also kann ein Teilchen mit sich selbst interferieren?! -
Der erste Schritt zur Beantwortung dieser Frage ist durch die obige Erklärung ja schon gemacht: Immerhin kann ein einzelnes Teilchen, das sich
dann etwa auf einer schleifen- bzw. schraubenförmig fortgeschriebenen Kreisbahn bewegt, auf diese Weise sogar allein durch einen Doppelspalt gehen, u. U. auch gleich mehrmals, was noch grundsätzlich
abgeklärt werden müßte.
Eine andere Möglichkeit wäre, so falsch dies zunächst klingen mag, daß immer erst im Zusammenwirken von zwei Teilchen die Photoplatte
geschwärzt wird, was ebenfalls den Schwarzschild-Effekt erklärte, d. h. die immer geringer werdende Empfindlichkeit bei abnehmender Strahlungsintensität.
Ein interessantes Ergebnis, das diese Frage ebenfalls berührt, liegt bereits seit einiger Zeit vor. Es handelt sich dabei um die
Feststellung, daß etwa bei Tunnelexperimenten, wie sie u. a. von Prof. Nimtz in Köln durchgeführt wurden, diejenigen Mikrowellen, die einen im Vergleich zu ihrer Wellenlänge zu engen Hohlleiter
durchlaufen hatten, danach zwar extrem abgeschwächt ankamen, die verengte Wegstrecke aber mit Überlichtgeschwindigkeit von bis zu 4,7 c durchtunnelt hatten.
Das paßt nun allerdings wieder hervorragend zum oben gegebenen Erklärungsmodell: Wenn die Mikrowellen (oder Photonen) beim Tunneln ihre
Kreisbahn nicht mehr vollenden können und – in seltenen Fällen – stattdessen an den Tunnelwänden reflektiert werden, kommt jetzt ihre offensichtlich größere Umlaufgeschwindigkeit zur Geltung und führt
direkt zur festgestellten Überlichtgeschwindigkeit.
>> Noch überzeugender sind jedoch womöglich die bereits,
zumindest teilweise, bestätigten Vorhersagen der Kernmechanik im Bereich der Kosmologie: Ausgehend von einem Koordinatensystem, dessen Bezugsachsen etwa durch die Rotationsachsen dreier aufeinander senkrecht stehender Kreisel definiert
seien, “sollten sich diese bis zu fernen Galaxien verlängerten Achsen auch “frei” in alle Richtungen (kein universelles Bezugssystem
!) verdrehen oder verbiegen können...” 3.
Tatsächlich wurde ein entsprechender Effekt, die Drehung der Schwingungsebene des Lichts ferner Galaxien,
schon beobachtet,- wie auch die beschleunigte Ausdehnung des Universums, welche als direkte Auswirkung der “Neutrinomasse” und ihrer am Rand des Universums anisotropen Richtungsverteilung interpretiert werden kann.
Dazu paßt ebenso das Auftreten der Gamma Ray Bursts im gleichen Bereich, was auf der jeweiligen Vernichtung (/Entstehung?) von sehr viel Masse beruht und offensichtlich nur am Rand des Universums vorkommt;- zum Glück für die Bewohner unserer Galaxie, denn Schwarze Löcher und Neutronensterne gäbe es ja auch in unserer Nähe. Im übrigen: wenn wie bereits festgestellt die bei Kernprozessen gebildeten Partikel asymmetrisch bevorzugt in Richtung Materie, statt Antimaterie zerfallen, warum sollte die uns umgebende Materie dann nicht kontinuierlich nach und nach auf diese Weise entstanden sein, statt durch einen Urknall?!
Festzuhalten bleibt: Wenn das dem Realistischen Kernmechanischen Modell zu Grunde liegende Erklärungsmodell zutrifft, was sich hier nun schon durch relativ einfache Experimente feststellen läßt, wäre damit zugleich auch das Problem der Vereinigung der vier Naturkräfte gelöst:
Die starke Kernkraft und die elektromagnetische Wechselwirkung beruhten grundsätzlich auf der selben Kraft, welche sich aber auf Grund
der besonderen Ladungsverteilung und Geometrie der Nukleonen, insbesondere aber auch wegen des auf einen kleineren Radius beschränkten Nukleonen-Spins – wie beobachtet – am Ende dennoch durchaus
verschieden auswirkten.
Die Neutrinos, welche nach neuesten Feststellungen offenbar doch ganz andersartige Teilcheneigenschaften besitzen, als bisher gedacht,
wären für die Übertragung der Kräfte verantwortlich, woraus sich nun für die Gravitation und die schwache Wechselwirkung weitere Folgerungen ergeben (bdw).
Dazu muß man außerdem sagen: So beeindruckend auch die Neutrinomessungen des Teams von Super-Kamiokande 11 erscheinen,- deren quantentheoretische Interpretation ist es aber nicht: Wenn nämlich nur halb so viele nach oben, wie nach unten gerichtete Myon-Neutrinos gefunden wurden, zugleich aber kein Überschuß an aufwärts fliegenden Elektron-Neutrinos, dann muß dies keineswegs bedeuten, daß sich die fehlenden Myon-Neutrinos nur in die kaum nachweisbaren hochenergetischen Tau-Neutrinos umgewandelt haben können.
Da bei einem anderen Experiment in Los Alamos anscheinend eine “Neutrino-Oszillation” von Myon-Neutrinos in Elektron-Neutrinos
festgestellt worden ist, sollte dieser Mechanismus auch bei Super-K zur entsprechenden Umwandlung geführt haben und somit nur die eigentlich fehlenden (siehe: Sonnen-Neutrinos) Elektron-Neutrinos
in diesem Fall durch umgewandelte Myon-Neutrinos ausgeglichen haben.
Wichtig scheint aber ebenso die jetzt experimentell gewonnene Erkenntnis, daß sich die einzelnen Neutrinoarten tatsächlich eher verhalten wie Photonen verschiedener Energie, die ohne weiteres ineinander übergehen können, als wie eigenständige Elementarteilchen!
Da Neutrinos offenbar viel häufiger mit Materie aller Art wechselwirken, ohne nun im klassischen Sinne gleich sichtbare
Teilchenumwandlungen auszulösen, sondern vielmehr nur jeweils einen winzigen Impuls übertragen und dabei Energie verlieren, sind sie damit auch die Träger der Gravitation. Die Abschwächung, welche sie
somit beim Durchgang durch Materie erleiden, führt dann dazu, daß ein anderer Körper im Sinne einer Abschattung dann aus dieser Richtung eine geringere (abstoßende) Krafteinwirkung, letztlich also
gerade eine Anziehung durch die erst genannte Materie, erfährt.
Den eher banalen Abschluß bildet die schwache Wechselwirkung, die im kleinsten atomaren Maßstab – analog zur Brown’schen
Molekularbewegung – nur ein Ausdruck ist für die momentan aus den verschiedenen Richtungen gerade auftretenden Kräfteschwankungen.
Ein Wort schließlich noch zur konkurrierenden herkömmlichen Quantenmechanik. Albert Einstein hat sie bekanntlich ein Leben lang
abgelehnt (”Gott würfelt nicht!”), die rein statistische Kopenhagener Deutung der Quantentheorie. Wenn nun die inzwischen gleichwohl als etabliert und bewiesen geltende Theorie vermehrt zu
seltsamen Konsequenzen mit nichtlokalen ”spukhaften Fernwirkungen” wie jetzt der sogenannten Quanten-Teleportation12 führt, so sind waren hierzu zwei unterschiedliche Standpunkte möglich:
Erstens der von Herrn Prof. Zeilinger, wonach wir eben zu akzeptieren haben, daß sich Quanten nun mal seltsam verhalten und ein verschränktes Photon
vom - möglicherweise Lichtjahre entfernten - anderen ”weiß”, wie es sich verhält und entsprechend instantan darauf reagiert...
Zweitens kann man aber auch fragen, ob denn die Voraussetzungen unter denen John Bell seinerzeit das nach ihm benannte Theorem
aufgestellt hat, wirklich in dieser Form zutreffen. Da es hierbei vor allem um die - unterschiedlich große - Korrelation zwischen jeweils verschränkten oder ”bloß” polarisierten Photonen geht, ist nun vielmehr kritisch nachzuprüfen, ob denn durch die verschiedenen Arten von Polarisatoren überhaupt eine ”vollständige” (z. B. lineare) Polarisierung der resultierenden Photonen erzielt werden kann!
Folgend den anschaulichen Modellen, wonach etwa die von einem elektrischen Dipol abgestrahlte Welle jeweils in zwei orthogonale
Teilwellen (bzw. Vektoren) aufgespalten werden kann, unterstellte man dergleichen einfach ebenso für die elektromagnetischen Lichtwellen, ohne sich noch Gedanken darüber zu machen, zu welchem Prozentgrad
(100, 90, 80 oder etwa gar 70%?) Photonen als Quantenteilchen nach dem Durchlaufen des Polarisators dann tatsächlich gleich ausgerichtet sind, wie das bei den zu 100 Prozent korrelierten verschränkten Photonen ganz zwangsläufig der Fall ist.-
Es muß doch möglich sein, mit überkommenen Vorurteilen aufzuräumen, wenn nun auch der Chefredakteur von Nature erklärt: “Wir haben schon Arbeiten zur Teleportation veröffentlicht, die eng mit den Grundlagen der Quantenmechanik zusammenhängen. Wenn es möglich ist, sie besser zu erklären, wäre das großartig. Aber am liebsten würde ich eine Arbeit publizieren, die zeigt, daß die Quantenmechanik ein Irrtum ist.”13
Schriften:
|