|
Voraussage von Meßergebnissen - Widerlegung von Fälschungen
Gerade Im Bereich der Schwerionenforschung - siehe hierzu auch die Seite: Kernmechanisches Modell - hat es schon seit längerer Zeit Vorwürfe zu der angeblich erfolgreichen Synthese der superschweren Elemente 118, bzw. 116 gegeben. Diese Fälschungsvorwürfe sind an Hand der Meßunterlagen inzwischen bestätigt worden, wo nämlich in die - an sich zunächst wenig aussagekräftigen - Originaldaten noch weitere - erfundene - Daten einer angeblichen Zerfallskette offensichtlich erst nachträglich eingefügt wurden.
Dies wirft natürlich auch die Frage auf, was denn das Kernmechanische Modell zu den tatsächlichen und vorgeblichen Meßdaten zu sagen hat. Selbstverständlich setzt das eine etwas aufwendigere Analyse im Einzelfall voraus, die sich aber im Vergleich zur ungleich aufwendigeren Messung dennoch in jedem Fall lohnt.
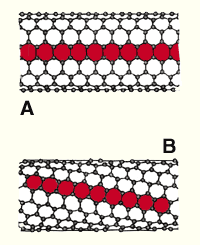
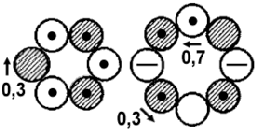
Für Blei wurde ja bereits auf der zuletzt erwähnten Seite eine kranzartige, innen offene Struktur mit zwei stabilisierende Knoten(-umschlingungen)
in der zu einem Ring geschlossenen Kette angegeben. Tatsächlich ist die hier gefundene Ringstruktur von Pb-208 oder Bi-209 geradezu prädestiniert dafür, mit einer weiteren, diesmal nur einfachen
Ringkette verschränkt zu werden.
Wie lang müßte also eine auf das obige Blei- oder Bismut-Target zu schießende Projektil-Kette sein, um sich ihrerseits gerade wieder um die erste
Ringstruktur schließen zu können? - Bei einer genaueren konkreten Kernmechanischen Modell-Überprüfung zeigt sich nun aber, daß das vom amerikanischen Ninov-Team gewählte Krypton-86-Nuklid viel zu
groß war, um diese Aufgabe ohne eine sofort erfolgende Spaltung überhaupt erfüllen zu können (womit der angebliche Erfolg also eine Fälschung sein mußte)!
Genau die richtige Länge hatte demgegenüber aber offenbar die Nickel-64-Projektilkette, welche bereits im Dezember 1994 bei der Darmstädter GSI auf ein Bi-209-Target geschossen wurde und zur erfolgreichen Synthese von Element 111-272 führte, welches dann nach etwa zwei Millisekunden zunächst in das Element 109-268 zerfiel und dieses dann wiederum in das mit fast 1,5 Sekunden Korrelationszeit schon relativ stabile Element 107-264.
Dies alles korrespondiert nun hervorragend mit dem Kernmechanischen Modell, was als Mindestlänge für
die erste Ringkette gerade 200 Nukleonen und für die zweite 64 Nukleonen fordert. Eine weitere Abspaltung eines Alpha-Teilchens verträgt die beschriebene Struktur dann jedoch nicht mehr, weshalb sich das
letztgenannte Element dann entweder spontan spaltet oder aber in zwei Stufen in das etwas anders aufgebaute Element Lr-256 (Korrelationszeit ca. 66 Sekunden) umwandelt.
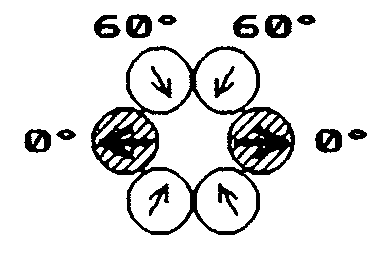
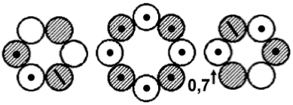
Der letztgenannte Kern sollte wiederum eine bleiähnliche Ringstruktur aufweisen, diesmal allerdings mit nunmehr drei, statt wie beim Blei zwei
stabilisierenden (Knoten-)Umschlingungen (und einer deutlich größeren Zugspannung) in der jetzt stärker in sich verdrehten Kette. Die Abbildung rechts oben steht übrigens für beide Kerne!
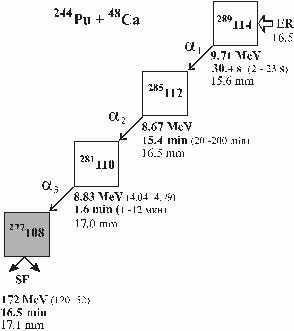
Es zeigt sich also, daß es nach allen kernmechanischen Überlegungen keine weiteren anders gearteten halbwegs stabilen Elemente mehr geben kann, wobei die letzte symmetrische und demzufolge bevorzugte Struktur wiederum mit dem in Dubna erzeugten Element 114 korrespondiert - das sich schließlich in das besonders stabile Element 108-277 umwandelte. Laut Kernmechanischem Modell liegt es bereits auf der Insel der Stabilität, die etwa bei A=272 beginnen sollte.
Dennoch darf man erwarten (und in diesem Fall auch hoffen), daß sich die ansonsten eher eitle Jagd nach dem “Weltrekord im Schwergewicht” damit
noch nicht zufrieden gibt und irgendwann einmal auch die - sicherlich weit weniger schwierige, als schwierig nachzuweisende - Synthetisierung etwa des Elements 128(!) angehen wird: Ganz analog zu dem
schon erwähnten und kernmechanisch vergleichbaren Vorbildprozess der erfolgreichen Synthese des Elementes 111 könnte das wiederum durch Ni-64-Projektile geschehen, die diesmal allerdings nicht auf ein Bismut-209-, sondern auf ein - sehr ähnlich strukturiertes - Fermium-257-Target (mit einer Halbwertszeit von ca. 100,5 Tagen) geschossen werden.
Sehr viel seltener als oben beschrieben würde dann u. U. aus dem zunächst erzeugten Compoundkern nach dem Abdampfen eines Neutrons das neue Element 128-320 entstehen, wobei die Zerfallskette hier voraussichtlich schon spätestens nach dem Abspalten von lediglich zwei Alpha-Teilchen enden müßte! Möglicherweise wäre dann aber die alternative Verwendung von Zn-70-Projektilen geeignet, um einen Ausweg aus den - keineswegs zu unterschätzenden(!) - Schwierigkeiten auf Grund des soeben angedeuteten Nachweisdilemmas im vorigen Fall aufzuzeigen.
KMO - Die Kernmechanischen Orbitale und die Supraleitung
Die meisten Physiker, welche sich heute - im 21. Jahrhundert - mit den Problemen der Supraleitung beschäftigen, sind ohne weiteres bereit zuzugeben, daß die grundlegenden Mechanismen hierbei noch immer nicht wirklich, sondern vielmehr erst ansatzweise verstanden worden sind.
Ist es womöglich gar kein Zufall, wenn sich an dieser Stelle die neue Kernmechanik in wichtigen Punkten von der alten Quantenmechanik unterscheidet?!
Letztere geht ja davon aus, daß sich bei entsprechend tiefen Temperaturen in (mehr oder weniger) großer Nähe zum absoluten Nullpunkt von Null
Kelvin oder ca. -273° Celsius - etwa in einer geeigneten Metallgitter-Struktur - Elektronen spontan zu sogenannten Cooper-Paaren mit (normalerweise) entgegengesetzter magnetischer Orientierung zusammenfinden, um sodann ohne Kollision mit den nur wenig angeregten Gitteratomen gemeinsam und widerstandslos ihren Weg durch das Gitter fortzusetzen...
Während die erwähnten “Cooper-Paare” auf Grund quantenmechanischer Überlegungen gemeinsam besonders energiearm und stabil sein sollen, verhält es sich bei zwei Elektronen, welche sich in einem (gesättigten und spingepaarten) Kernmechanischen Orbital aufhalten, etwas anders; - und doch auch wieder nicht. Zumal ja in der Quantenmechanik - Stichwort: Pauli-Prinzip - ebenfalls Atom- und Molekül-Orbitale bekannt sind, die gleichermaßen mit maximal zwei Elektronen unterschiedlicher Ausrichtung besetzt sein dürfen. Allerdings gilt das eben nur für die genannten Atom- und Molekül-Orbitale und nicht für freie Elektronen.
Worin unterscheiden sich Quantenmechanik und Kernmechanik nun aber voneinander? Zur Erinnerung: In der Kernmechanik bewegen sich laut Kernmechanischem Modell bekanntlich ”alle im Atom vorkommenden Elementarteilchen wie Protonen, Neutronen, Elektronen, Photonen und ihre Antiteilchen ... auf genau definierten Bahnen, bei Abwesenheit sonstiger Felder: auf - durch Neutrinos und Teilchenspin bewirkten - Kreisbahnen, jeweils um ihren eigenen (zeitlich gemittelten, in Wirklichkeit aber leeren) virtuellen Schwerpunkt.”
Wie schon weiter oben beschrieben, können sowohl Nukleonen-Orbitale in den Kernringen und ebenso Elektronen-Orbitale im Atom und außerhalb(!) dann (nach und nach) jeweils auch doppelt besetzt sein, wenn bereits alle zur Verfügung stehenden Orbitale (einfach) besetzt sind. Als ein wichtiges Beispiel für solche doppelt besetzten Elektronen-Orbitale wurden speziell die aromatischen Verbindungen des Kohlenstoffs genannt.
So befinden sich z. B. jeweils drei mit zwei Elektronen abgesättigte Orbitale in jedem Benzolring, weshalb das diamagnetische Benzol folglich ein guter Isolator ist. Graphit sowie “gerade” strukturierte Nanotubes mit in der Regel einfach besetzten Orbitalen sind, soweit sich die Elektronen ungehindert in ihrer Bahnebene bewegen können, gute, bzw. sogar “metallische” Leiter. Was aber macht dann den guten Supraleiter aus?
Nun, er vereinigt die besten der vorgenannten Eigenschaften: Zum einen sollen die Elektronen-Orbitale möglichst doppelt besetzt sein, aber eben
nicht alle; d. h. es muß zum - verlustfreien - Doppel-Ladungstransport auch Löcher geben, damit ein Strom überhaupt erst fließen kann. Es ist dies also eine sehr kritische Balance zweier komplementärer, sich gegenseitig beinahe ausschließender Parameter - und dabei alles perfekt in einer Ebene (praktisch in mehreren parallelen Ladungsstreifen).
Daß die kernmechanischen Überlegungen wahrscheinlich richtig sind, darauf deutet ein sehr pfiffiges und aussagekräftiges Experiment, welches die Folgen einer Ladungsträgeränderung unmittelbar durch das Anlegen einer elektrischen Spannung an eine Steuerelektrode beeinflussen und messen konnte, wobei die Materialprobe aus Calciumkupferoxid vom Nichtleiter
zum Hochtemperatursupraleiter geregelt werden konnte.
Was dann die weiteren schon erfolgreich erprobten oder auch gerade erst angedachten Hochtemperatursupraleiter, etwa auf der Basis des sehr
einfachen Magnesiumdiborid oder von Lithiumborocarbid anbelangt, kann hier die Kernmechanik wertvolle Aufschlüsse über die 3D-Strukturen dieser Verbindungen liefern. Dabei ist allerdings zu beachten, daß neben den gerichteten Valenzelektronen hierbei die kernbedingt festgelegten Ebenen der anderen Elektronen - und somit etwaige Isotopie-Unterschiede wie etwa zwischen O-16 und O-17 bzw. O-18 - ebenfalls eine wichtige Rolle (z. B. bei Li-6 und Li-7) spielen können.
Ganz sicher lohnen die durch sorgfältiges Struktur-Design erzielbaren Fortschritte bei der wirtschaftlich enorm wichtigen Erhöhung der nutzbaren
Sprungtemperatur jede Anstrengung; - und sei es um den Preis, sich auch mal von alten Vorurteilen zu trennen.
KMO - Ein ideales Modell der chemischen Bindungen
Heute wie vor (über) hundert Jahren ist allzuviel kreative und progressive Phantasie in der Chemie - zumindest anfangs - noch selten sehr
erwünscht. Dies mußte damals auch schon der später hoch geachtete und geehrte Begründer der Stereochemie, Jacobus Henricus van’t Hoff erfahren. Sein Chemiker-Kollege Hermann Kolbe bezeichnete jedenfalls die vom Holländer erfundene Tetraeder-Theorie der räumlich spiegelbildlich angeordneten Kohlenstoff-Liganden als “nicht weit entfernt von Hexenglauben und Geisterklopfen”.
Auch wenn man sich heute die etablierte Physikalische Chemie (auf der Grundlage der alten Quantenmechanik) einmal genauer ansieht,
wird man schnell feststellen, daß es dort noch immer zahlreiche Denkmodelle und Rezepte gibt, welche eher an die - zwar durch Erfahrungswerte stark verbesserte - alte Alchimie erinnern, als an eine moderne Wissenschaft.- Natürlich nicht in dem Maße wie bei der “Moderne(n) Alchemie” auf der ”Jagd nach den schwersten Elementen” (Münzenberg
und Schädel, Vieweg Verlag), - also bei der Schwerionenforschung oder noch mehr bei der physikalischen Grundlagenforschung, aber dennoch...
Manch einem wird dies bei dem hohen Stand heutiger Chemie-Forschung und -Technik vielleicht übertrieben polemisch erscheinen, - jedoch läßt sich
die Behauptung ohne Schwierigkeiten belegen:
Da wäre zunächst einmal der Effekt der Mesomerie mit sogenannten delokalisierten Elektronen bei bestimmten Verbindungen, wo sich die tatsächlichen Bindungsverhältnisse nur innerhalb von - nicht existierenden - Grenzstrukturen mit Hilfe sogenannter Resonanzen zwar handhaben, aber nicht wirklich erklären lassen. Zum anderen ist eben auch die sogenannte sp3-Hybridisierung
des Kohlenstoffatoms, obwohl sie vielen Chemikern fast schon als eine bewiesene und bewährte Tatsache erscheinen mag, in Wirklichkeit eben nur ein Denkmodell, welches allein dazu dienen soll, die an
dieser Stelle eigentlich unpassende alte MO-Theorie wiederum an die Tatsachen anzupassen, siehe ebenfalls: Die Kernmechanischen Orbitale von Bor und
Kohlenstoff.
Allerdings müssen nun im Licht der inzwischen gewonnenen Erkenntnisse auch beim Kernmechanischen Modell einige Fehler korrigiert werden (was aber nicht mit der eben kritisierten eher willkürlichen Anpassung der Theorie an die Tatsachen zu verwechseln ist. Wie man nämlich gleich sieht, wird die Theorie der Kernmechanischen Orbitale (KMO) dadurch eben nicht verbogen, sondern vielmehr in sich deutlich konsistenter!).
Demnach verhält es sich bei den Orbitalen des Kohlenstoffs nicht anders, als bei allen anderen Atomen - mit Ausnahme von Wasserstoff -
auch:
Die inneren beiden “s”-Elektronen sind derart eng an den Kern gebunden, daß sie unmittelbar nicht zu den sogenannten Valenzbindungen beitragen. Gleichwohl spielt es durchaus eine Rolle, welche
Elektronen sich jeweils auf welchen Kernmechanischen Orbitalen wo befinden.
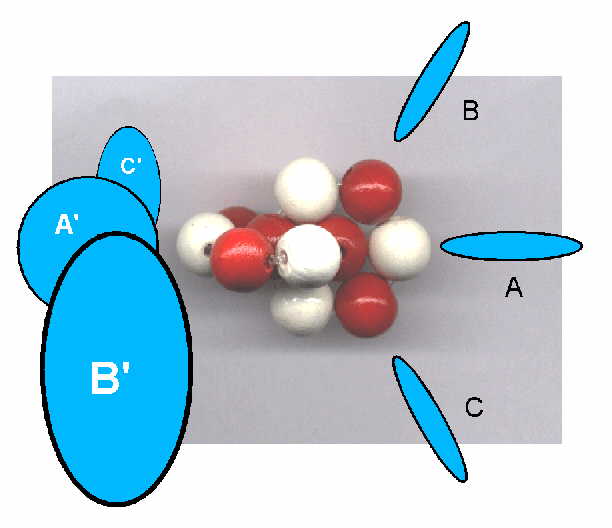
Beim Kohlenstoffatom gibt es demnach grundsätzlich zunächst sechs verschiedene (von den Nukleonen beider Kernringe bestimmte) Orbital-Ebenen, in
denen sich Elektronen aufhalten können. Jedem der beiden (senkrecht zueinander stehenden) Kernringe sind dann drei Orbitale A, B und C, bzw. A’, B’ und C’ zugeordnet.
Da, wie erwähnt, zwei Elektronen den Kern innen eng umkreisen, bleiben im Kohlenstoffatom genau vier Orbitale übrig, die folglich mit
Valenzelektronen besetzt sein können. Beim Diamantgitter und ebenso beim Methan sind dies die Orbitale B, C, B’ und C’. Im letzten Fall sind die vier Wasserstoffatome in den Eckpositionen somit völlig
frei, um sich nun im energetisch günstigsten Tetraederwinkel von 109° 28’ einzustellen.
Beim Graphit und beim Benzol verhält es sich bekanntlich anders, da hier die Elektronen der Orbitale B, C sowie A (welches sich gegenüber der gezeichneten Anordnung nun auf der anderen Seite des Atomkerns befindet) drei “Sigma”-Bindungen betätigen, während das vierte quasifreie Elektron A’ in der Zeichnungs- bzw. Molekül-Ebene (bei Benzol) gepaart oder (bei Graphit) ungepaart für die “Pi”-Bindungen zuständig ist.
Die wichtigste der oben angekündigten Modellkorrekturen bezieht sich dann auf eine andere wichtige Bindungsklasse des Kohlenstoffs, nämlich die
Doppelbindungen. Natürlich sind hier, wie es eigentlich normal ist - was ist beim Kohlenstoff schon “normal”(?!), - pro Atom nur zwei Elektronen daran beteiligt, also etwa A (= axial) und B. Die
Valenzrichtung wird bestimmt von der axialen Sigma-Bindung, welche durch das zweite Elektronenpaar beider Atome noch zusätzlich verstärkt wird.
Im O2-Molekül steht übrigens das zweite an der Doppelbindung beteiligte Elektron jeweils im rechten Winkel nach außen weg. D. h. das
zweite Elektronen”paar” ist nicht miteinander verschränkt und somit für den Paramagnetismus des Sauerstoffs verantwortlich.
Es ist nun völlig klar, daß die Kohlenstoff-Doppel- und Dreifachbindungen auf Grund der ungünstig benachbart angeordneten Elektronen-Orbitale
nicht so stabil sein können wie die Einfachbindungen. Aber gerade das macht ja eben die Bindungsvielfalt der Kohlenstoffchemie aus! Das absolute Gegenbeispiel hierzu, das reaktionsträge Stickstoffmolekül
mit seinen “bombenfesten” Dreifachbindungen erstaunt demgegenüber auf den ersten Blick. Ist doch Stickstoff kernmechanisch, s. o., praktisch identisch aufgebaut wie Kohlenstoff.
Der entscheidende Unterschied liegt jedoch in dem jetzt zweifach besetzten Elektronen-Orbital A’, weshalb nun das freie Elektronenpaar A’ alle
drei Valenzbindungs-Orbitale A, B und C - wie in der Zeichnung dargestellt - auf eine (d. h. die andere) Seite des Atoms zwingt. Interessant sind in diesem Zusammenhang nun die Stickoxide. Bekanntlich variieren ja bei NO2 in Abhängigkeit von der Ladung nicht nur der mittlere Bindungsgrad sondern auch der jeweilige Bindungswinkel vom positiv geladenen Nitryl-Kation über das neutrale Stickstoffdioxid bis zum negativ geladenen Nitrit-Kation von 180° über 134° bis zu 115°.
In der quantenmechanisch ausgerichteten Physikalischen Chemie wird dies einfach mit der wachsenden Abstoßung durch zunächst ein freies Elektron und schließlich ein freies Elektronenpaar erklärt. Das ist zwar kernmechanisch nicht ganz falsch, aber auch nicht ganz richtig: Beim Nitrit-Anion binden etwa die beiden Sauerstoffatome tatsächlich an die beiden Stickstoff-Orbitale B und C, wobei noch ein Elektron vom A-Orbital abgezogen wird und vom einen (stark elektronegativen) Sauerstoffatom gebunden wird, während das zweite Sauerstoffatom noch ein weiteres Elektron von außen aufnimmt. Auf der anderen Seite des Stickstoffatoms ist auch das Orbital A’ mit zwei Elektronen besetzt.
Wenn man nun die beiden - ohne die bindenden Elektronenpaare auf den Orbitalen B und C - neutralen(!) Sauerstoffatome aus der Rechnung entfernt,
bleiben auf den Orbitalen B, C und A’ jeweils drei “freie” Elektronenpaare übrig, deren Bindungswinkel leicht (erklärbar) von den grundlegenden 120° der Orbitale abweicht.
Befindet sich bei Stickstoff-Dioxid nun nur noch ein Elektron auf dem Orbital A’, so vergrößert sich der Bindungswinkel - ebenfalls gut
nachvollziehbar - von 115 auf 134°. Lediglich beim Nitryl-Kation verhält es sich insofern etwas anders, als hier die Sauerstoffatome nicht an die Orbitale B und C, sondern an A und A’ koppeln, was
logischerweise einen Bindungswinkel von exakt 180° zur Folge hat. Ebenso leicht läßt sich auch der Aufbau der linearen aber asymmetrisch strukturierten N2O-Molekel aufklären: An ein ganz
normales Stickstoffmolekül mit einer Dreifachbindung über die Orbitale A, B und C “hängt” auf der anderen Seite an A’ einfach nur noch ein zusätzliches Sauerstoffatom mit der zuvor schon beschriebenen
sauerstofftypischen Doppelbindung, wobei die Stabilität der Verbindung durch die zusätzliche Kernladung naturgemäß geschwächt erscheint.
Nachdem nun durch das Abarbeiten von einigen allen Chemikern bekannten Sauerstoffverbindungen des Stickstoffs hoffentlich ein wenig Vertrautheit
mit der neuen KMO-Theorie erreicht werden konnte, soll anschließend noch das besonders interessante Kohlenmonoxid-Molekül behandelt werden.
Auf Grund der eingezeichneten Orbitale ist vielleicht nicht ohne weiteres zu ersehen, wie sich diese mit der genannten Verbindung vereinbaren
lassen und doch ist dies möglich: Wenn nämlich ein Sauerstoffatom an das Kohlenstofforbital B ankoppelt und dabei noch das C-Elektron an sich bindet, muß auch das A-Orbital auf die gegenüberliegende
Seite des Atoms ausweichen - wo sich bereits das Orbital A’ befindet. Die Elektronen beider Orbitale bilden jetzt, trotz unterschiedlicher Spinausrichtung, dennoch ein quasi spingepaartes, freies
Elektronenpaar, das anderen Atomen gegenüber - zunächst - weitgehend abgesättigt erscheint...
An dieser Stelle soll nun nochmals auf das quantenmechanische Konstrukt der sp3-Hybridisierung eingegangen werden. Kernmechanisch sind die vier Valenzelektronen des Kohlenstoffs oder die drei Valenzelektronen des Bors (mit ihren Elektronenmangel-Verbindungen - da die Zahl der Orbitale die der Elektronen übersteigt!) nämlich der Normalfall und keineswegs die Ausnahme - und verlangen eine entsprechende Korrektur der Hund’schen
Regeln. Eine Ausnahmestellung steht vielmehr dem Sauerstoff zu, wo dann nämlich sechs Valenz- oder besser L-Elektronen auf nur vier Orbitale kommen (O-16).
Für O-18 (und ebenso O-17) gilt das Modell von O-16 jedoch nicht mehr, sondern vielmehr das bereits weiter oben vorgestellte Kernmechanische
Basismodell von C-12, welches demgegenüber sechs Orbitale aufweist, auf die jetzt sechs L-Elektronen zu verteilen sind. Anders als beim Stickstoff, mit nur einem freien Elektronenpaar im Orbital A’, ist es nun jedoch offenbar energetisch günstiger, wenn die beiden freien Elektronenpaare auf B’ und C’ verlagert werden, wodurch ganz zwanglos (die “Tetraederecken”) B und C für die bindenden Elektronen übrig bleiben.- Alles in allem also - trotz des andersartigen Kernmodells -
dennoch ein “typisches” Sauerstoffatom, dessen feine Unterschiede gleichwohl unbedingt nachweisbar sein müßten!
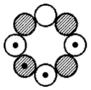
Ganz analog zum C-12-Basismodell, mit den insgesamt dort vorhandenen sechs Elektronen-Orbitalen, ergeben sich auch für das in der Fig. 5b, oben,
aufgeführte Kernmechanische Modell von O-17 und F-17 (vergl. hierzu: Kernmechanisches Modell - neu) insgesamt wiederum genau sechs Orbitale.
Von daher könnte das genannte Modell also richtig sein (natürlich ebenso das von C-12 abgeleitete...). Wenn man in der vorgenannten Struktur nun aber den mittleren 6er-Ring durch einen
Be-8-Kernring ersetzt, was rein rechnerisch, auch beim Dipolmoment, exakt zum F-19-Nuklid führt, so ergäbe das in diesem Fall - drei plus vier - insgesamt sieben Orbitale; - was auf den ersten
Blick kaum mit den chemischen Eigenschaften eines Halogens vereinbar scheint.
Bliebe demnach nur das C-12-Basismodell - mit sieben doppelt besetzten Nukleonen-Orbitalen -, welches ebenfalls besser den “verbotenen” Übergang
von F-19 zum etwas anders strukturierten Ne-20-Nuklid erklärte. Andererseits sind die angegebenen Elektronen-Orbitale ja keineswegs starr, sondern eher flexibel. Dies erhöht ganz sicher auch den
Spielraum für eine mögliche Verschmelzung der Orbitale miteinander.
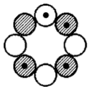
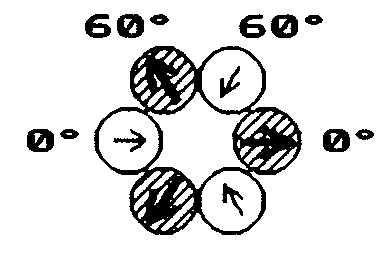
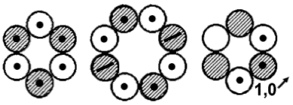
Ne-20 und die folgenden auf der Ne-20-Grundstruktur aufgebauten Kerne - Ausnahme Mg-24 - verfügen entgegen dem ersten Anschein dann jedoch
gleichermaßen und ganz “regelgerecht” wiederum über insgesamt sechs Elektronen-Orbitale, da, wie die Abbildung rechts oben zeigt, nun zwei Orbitale - senkrecht zur Nuklid-Hauptachse - jeweils zu einem
einzigen Orbital zusammenfallen.
Vorläufiger Schluß und Kernspin-Lösung
So gut obiges C-12-Basismodell jetzt auch zu den darauf aufbauenden Folgekernen C-13 bis O-15 passen mag, die Dipolmomente von O-17 bis Ne-19 kann
es offenbar nicht erklären! Dies gelingt jedoch mit Hilfe eines anderen, schon früher vorgestellten Kernmodells und dessen Zentralstruktur von elf zu einer “liegenden Acht” verschmolzenen Nukleonen - wo
das mittlere (von beiden 6er-Kernringen quasi gemeinsam genutzte) Nukleon das Dipolmoment praktisch alleine bestimmt;- siehe: Kernmechanisches Modell - neu
Tatsächlich entspricht das gemessene magnetische Dipolmoment von F-19 mit 2,6287 MK fast genau dem des einzigen
ungepaarten Protons (2,793 MK) und Ne-19 mit -1,886 MK gleichfalls dem des einzigen ungepaarten Neutrons (-1,913 MK). Wie geht es dann aber weiter? Eigentlich sollte man ja erwarten, daß von Ne-21 ab -
womöglich bis zu Ca-40 - nunmehr das neue Ne-20-Basismodell auch für die Folgekerne bestimmend sein würde. - Offenbar ist dies jedoch nicht so!
Nach einer umfassenden Analyse und - systembedingt - mancherlei Irr- und Umwegen bleibt anscheinend nur eine mögliche Schlußfolgerung übrig:
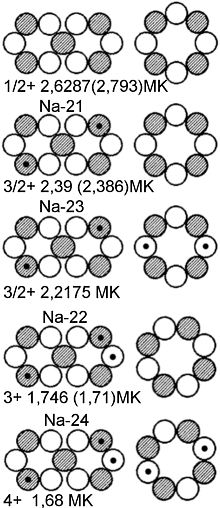
Während Ne-21 (mit -0,66176 MK) - wie erwartet - auf dem genannten Ne-20-Kernmodell basiert, gründet sich der vorgebliche Spiegelkern Na-21 auf das andersartige Kernmodell (deshalb hier die Gamma-Reaktion!)
von F-19, dem lediglich noch zwei spingepaarte Protonen zugefügt wurden - wodurch sich das Dipolmoment um ca. 0,2 MK auf 2,39 MK reduziert. Eine weitere Abnahme des Dipolmoments in gleicher Größenordnung
ergibt sich schließlich nach nochmaliger Zugabe zweier spingepaarter Nukleonen, diesmal Neutronen, bei Natrium-23 mit einem gemessenen Dipolmoment von 2,21751 MK.
Die Einordnung und Berechnung der anderen Kern-Momente erfolgt nach dem gleichen o. g. Schema: So erhält man aus dem Dipolmoment von Na-21 (2,39
MK) auch dasjenige von Na-22 (1,746 MK), wenn man jetzt etwa 0,7 MK - für ein weiteres Neutron in einem nunmehr doppelt besetzten Orbital - von dem ersten abzieht (oder mit 1,68 MK ebenso das von Na-24, wenn außerdem nun noch zwei spingepaarte Neutronen
hinzukommen). - Das F-20-Nuklid (2,092 MK) könnte sodann ebenso aus F-19 (2,6287 MK) hervorgegangen sein oder Mg-25 (-0,85512 MK) aus Ne-21 (-0,66176 MK), usw., usw. -
Mit Hilfe der neuen Erkenntnisse können nun auch die bisher vorhandenen großen Schwierigkeiten bei der Behandlung einiger leichterer Atomkerne
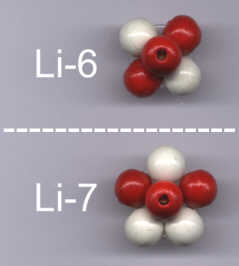
überwunden werden. Dabei zeigt es sich alsbald, daß genau jenes schon früher gefundene (und dann verworfene) Kernmechanische Modell von Li-6 (0,822010 MK) mit einem He-4-Kernring und einer Deuterium-Achse doch das richtige sein muß; zumal die Kerne Li-8 (1,653 MK und 2+?) und Be-9 (-1,1774 MK) - sowie C-11(?!) - ebenfalls wieder darauf aufbauen.
Allem Anschein nach ist es jedoch bei den Messungen der Eigenschaften des Li-8-Kerns zu einer Verdopplung der Meßwerte gekommen!(?!) Nach Addition
zweier spingepaarter Neutronen sollten Kernspin und Dipolmoment hier nämlich genau denen von Li-6 (0,822 MK und 1+) entsprechen!- Ganz und gar regelgerecht ist das Ergebnis dann aber,
wenn bei Be-9 (auf Grund des jetzt doppelt besetzten Orbitals) wiederum 0,322 MK zu den 0,857406 MK der Deuterium-Achse hinzukommen. Folglich ist die Summe nun (-)1,1794 MK.
Nachdem somit viele Kerne mittlerweile grundsätzlich richtig eingeordnet werden konnten, verbunden mit der Berechnung ihrer wichtigsten Parameter,
ist es jetzt an der Zeit, bisherige Annahmen und Hypothesen (wie die schon einmal verworfene radiale Spinanordnung) versuchsweise erneut auf den Prüfstand zu stellen. Was also. wenn sich letztlich doch herausstellte, daß Spin und Dipolmoment - nach den Gesetzen sonstiger physikalischer Logik - auch beim Kernmechanischen Modell parallel zueinander orientiert wären?
In diesem Fall führte dann die Natur der starken Kernkraft - wie ursprünglich angenommen - in der Regel zu einer (manch einem vielleicht etwas banal erscheinenden) konjugierten Anordnung der Nukleonen in den Atomkernen bzw. Kernringen;- also immer abwechselnd ein Proton und ein Neutron. Demgegenüber hätte nun - entgegen der obigen Annahme - die kleinere Spinpaarungsenergie letztlich doch keine primäre ordnende Funktion. D. h. auch Kohlenstoff wäre im Grundzustand von C-12 aufgebaut wie im Foto oben dargestellt, nur daß jetzt zwei Neutronen innen sein sollten und nicht wie dort abgebildet zwei Protonen (2. angeregter Zustand). -
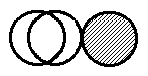 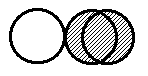 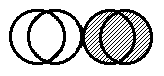
Die korrigierte Abbildung zeigt von links nach rechts:
das Kernschema von C-13, N-13 und N-14
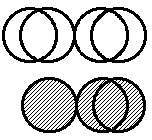 
Kernschema von N-15 und O-15
Man könnte nun annehmen, daß es beim Auftreten von mindestens zwei doppelt besetzten Kernring-Orbitalen dann zu einer Umgruppierung der
Grundkonfiguration des Kohlenstoff-Nuklids käme - von den ursprünglichen zwei Li-6-Ringen hin zu je einem He-6- und einem Be-6-Kern (wobei die
ersten beiden bzw. die zweimal gleichnamig doppelt besetzten Orbitale immer in einem Ring einander gegenüber angeordnet wären).- Plausibler
ist hier aber ein Kernmodell auf der Basis von O-16, bei dem jetzt jedoch ein einziges Orbital noch nicht doppelt besetzt ist. Dafür spricht allein schon die
besonders große Bindungsenergie von N-15, verbunden mit einem auffällig kleinen Wirkungsquerschnitt für thermische Neutronen von lediglich 0,00002 Barn.
Natürlich darf man an dieser Stelle noch nicht erwarten, daß jedes zuvor angegebene Modell im Einzelfall auch immer schon das richtige ist. Die
Wahrscheinlichkeit dafür steigt jedoch mit der Anzahl der erfüllten Kriterien: So “stimmt” etwa beim obigen Modell von Na-23 zwar das magnetische Dipolmoment, der manchmal - wie im Fall von Li-8 - mit etwas Vorsicht zu
betrachtende Kernspin aber womöglich nicht.
Anders ist das aber, wenn man hier die Grundstruktur der aus elf Nukleonen
bestehenden “liegenden Acht” durch eine solche mit fünfzehn Nukleonen ersetzt, also durch zwei miteinander verschmolzene 8er- statt 6er-Ringe.
Der mit dieser Struktur verschränkte 8er-Ring hätte dann analog zu Mg-24 ebenfalls nur noch einfach besetzte Orbitale, was wiederum ausgezeichnet mit der von Ne-22 über Na-23 zu Mg-24 steigenden Bindungsenergie korrespondiert.
Außerdem wird nun am Kernmechanischen Modell unmittelbar deutlich,
daß die beiden sehr ähnlichen Übergänge von F-19 zu Ne-20 bzw. von Na-23 zu Mg-24 nicht deshalb so selten sind, weil sie etwa aus Gründen der Paritätserhaltung formal verboten wären, sondern weil es kernmechanisch eben fast ausgeschlossen ist, zwei “siamesisch” verschmolzene Kernringe
mit einem mittleren, beiden Kernringen gemeinsamem Nukleon - durch die Zufuhr eines Protons von außen - ohne weiteres wieder in zwei getrennte Kernringe umzuwandeln.
In jedem Fall erscheint das inzwischen wesentlich weiter entwickelte und verbesserte Kernmechanische Modell mittlerweile derart schlüssig und
zutreffend in der Beschreibung der Fakten und ihrer Ableitung unmittelbar aus dem Modell, daß nunmehr die weitere Überprüfung von Voraussagen des Modells dringend geboten erscheint:
Z. B. die Verifizierung der prognostizierten (relativ geringen) chemischen Bindungsunterschiede zwischen O-16 sowie O-17 und O-18, außerdem
aber auch zwischen den beiden stabilen Kohlenstoff-Isotopen C-12, C-13 und C-14 (Be-8-Kernring +6) bzw. dem kurzlebigen Kohlenstoff-Isotop C-11,
das nach seinem Dipolmoment ebenfalls aus nur einem Kernring (Li-6 mit fünf doppelt besetzten Orbitalen) besteht!
Modell-Überprüfung durch Dipol-, Quadrupol- und Trägheitsmomente
Die wirksamste Möglichkeit zur Verifizierung der Grundaussagen des Kernmechanischen Modells liegt jedoch vor allem in der zusätzlichen
meßtechnischen Erfassung bislang noch unbekannter Dipolmomente und der anschließenden Analyse, ob, bzw. wie gut dann Messungen und Modell -
möglichst ohne weitere Modell-Anpassungen(!) - letztlich übereinstimmen.
In der Tat gibt es mittlerweile zumindest eine neue Dipolmoment-Messung,
die sich für den genannten Zweck eignet und somit gleich zur Überprüfung herangezogen werden soll: das Dipolmoment von Mg-23, das nunmehr mit 0.536 MK bestimmt wurde.
Weiter oben ist ja u. a. schon das direkt von Ne-20 abgeleitete Nuklid Ne-21
mit -0,66176 MK aufgeführt, zu welchem jetzt - beim zentralen Be-8-Ring - lediglich zwei weitere Protonen hinzugefügt werden. Der neue Meßwert
(Kernspin: J = 3/2) paßt somit bestens ins Bild - sogar besser noch, als das vorher schon erwähnte Mg-25 (J = 5/2!) mit -0,85512 MK.
Schon jetzt wird aber eine (offenbar durchweg geltende) Gesetzmäßigkeit erkennbar, nach der die gemessenen Dipolmomente der Kerne gegenüber
dem aus der Nukleonenanordnung unmittelbar abzuleitenden Dipolmoment prozentual jeweils umso kleiner ausfallen, je schwerer der betreffende Kern
tatsächlich ist: Verglichen mit dem theoretischen Wert von 0,88 MK, der sich aus der reinen Addition der Dipolmomente von Proton und Neutron ergibt,
ist das gemessene magnetische Moment von Deuterium um 2,63 % kleiner, das von Lithium-6 (bzw. Lithium-8, - s. o.) jedoch sogar um 7,05 % (bzw. 6,47 %).
Auch die bereits erwähnte, bei C-13 (0,702381 MK) beginnende, sodann über O-15 (+/- 0,719 MK) und Ne-21 (-0,66176 MK) mindestens bis zum
Nuklid Mg-23 (0,536 MK) reichende Reihe wirkt auf den ersten Blick sehr eindrucksvoll. Kritischerweise muß hierzu aber angemerkt werden, daß zwar
das Dipolmoment von Ne-21 gegenüber dem von C-13 sehr realistisch um 5,78 % vermindert erscheint, daß aber ein Wert von -30,6 % bei Mg-23 -
anders als bei Si-29 ( -26,1 %) - auch auf die Deformation der Kernringe zurückzuführen ist.
Ein Extrembeispiel für die große Empfindlichkeit eines Dipolmoments gegenüber der Deformation von Kernringen bietet der Al-27-Kern, der
grundsätzlich wie F-19 aufgebaut ist, nur daß jetzt alle Orbitale des 8er-Kernrings in diesem Fall mit je zwei Nukleonen (doppelt) besetzt sind!
Allein dies reicht aus, um das durch zwei miteinander verschmolzene 6er-Kernringe (“liegende 8”) mit einem gemeinsamen mittleren Proton
erzeugte Dipolmoment von den bei F-19 gemessenen 2,6287 MK bei Al-27 zugleich mit der genannten Struktur quasi auch in der Größe auf 3,6414 MK zu “dehnen”.
Im übrigen ist die kernmechanische Erklärung für die mit dem jeweiligen Atomgewicht verbundene Reduzierung der gemessenen Dipolmomente
sehr einfach und einsichtig: Da ja bei allen einschlägigen Verfahren zur Bestimmung der magnetischen Dipolmomente bei deren Umklappen immer
auch der gesamte Kern mit(um)gedreht werden muß, ist dieser Vorgang nach den Regeln der Mechanik natürlich auch an das Trägheitsmoment des betreffenden Körpers, in diesem Fall des Atomkerns, gebunden.
Nach den magnetischen Dipolmomenten, die bei allen Überlegungen bis jetzt wohl die größte Rolle gespielt haben und den soeben erwähnten Trägheitsmomenten, soll es nun vor allem um die Quadrupolmomente der
Atomkerne gehen, die ja - mit wenigen Ausnahmen - fast durchweg positiv, d. h. prolat oder zigarrenförmig sind. Es gibt hier nur wenige “negative” oblate oder diskusförmige Ausnahmen - etwa O-17 und Al-27.
Für O-17 wurde aber bereits festgestellt, daß in diesem Fall nur ein einziges
Kernmodell in Frage kommt, nämlich eine 11-Nukleonen-Grundstruktur aus zwei miteinander verschmolzenen 6er-Kernringen, die sich nun das mittlere
Nukleon (ein Neutron) teilen, welches dann vom zweiten 6er-Kernring einge- bzw. umschlossen wird.
Interessanterweise ergibt sich für diesen Kern in jedem Fall ein negatives Quadrupolmoment, unabhängig davon, ob - wie zuletzt angenommen - Spin
und Dipolmoment (bei einem tangentialen Kernspin parallel) in die gleiche Richtung weisen oder (bei einem radialen Kernspin) senkrecht zueinander
orientiert sind. Warum sollte man sich also noch länger mit der vom “alten” Kernmechanischen Modell entliehenen Elektronen-Magnetismus-Theorie befassen (von der dann der radiale Kernspin abgeleitet wurde), wenn es
auch “ohne” geht;- zumal man bei einer Analyse des Al-27-Kerns ebenso zu dem nämlichen Ergebnis gelangt?!
Eine zunächst unüberbrückbare Schwierigkeit bietet dann jedoch die zuletzt für Na-23 angegebene 15-Nukleonen-Grundstruktur, wo nun sogar beide
Kernspin-Varianten versagen. Nach einigen Irritationen kommt man aber in diesem speziellen Fall letztlich doch zu dem wiederum sehr befriedigenden
Ergebnis, daß das vorige, von F-19 abgeleitete, Kernmodell nicht nur zum richtige(re)n Dipolmoment führt, sondern überhaupt das richtige sein muß!
Zum einen ist das soeben verworfene 15+8-Nukleonen-Modell allein schon kernmechanisch gesehen sehr instabil, zum anderen gibt es beim richtigen
Modell nun ebenso eine optimale Spinpaarung, die wiederum zur maximal möglichen Bindungsenergie führt.
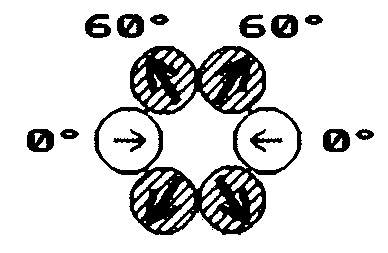
Da jedoch hieraus noch immer keine Entscheidung abzuleiten ist, ob beim Kernmechanischen Modell die Dipolmomente nun tangential oder radial zu
den Kernringen ausgerichtet sind, kann jetzt womöglich eine Analyse des B-10-Nuklids genaueren Aufschluß über diese Frage geben. Zunächst einmal: Gibt es auch bei tangentialer Ausrichtung der Dipolmomente (mit paralleler Dipolmoment-Spin-Orientierung) für B-10 ein Kernmechanisches
Modell mit verschränkter (nicht “Sandwich”-) Anordnung der Kernringe, wo ebenfalls das Ergebnis stimmt?
Die Antwort ist: fast; aber letztlich eben doch nicht ganz bzw. nicht gut genug.
Entweder ist nämlich das resultierende Dipolmoment in einem Fall deutlich zu klein oder im anderen Fall wiederum deutlich zu groß. Noch gravierender
stellen sich diese Probleme aber bei der Dipolmoment-Berechnung etwa von F-17 dar, wo es offenbar überhaupt nicht mehr gelingt, ohne radiale
Spin-(genauer gesagt: Dipolmoment-)orientierung und spinkompensierte Kernringe (mit einander gegenüber liegenden gleichartigen Nukleonen) zu einem richtigen Ergebnis zu gelangen.
Schier unüberwindlich werden die mit einer parallelen Dipolmoment-Spin-
Orientierung verbundenen Schwierigkeiten aber bei vielen gg-Kernen, wo das Dipolmoment ja immer Null sein muß, z. B. bei Be-10. Ohne die
symmetrische Anordnung von zwei verschränkten He-5-Kernringen gibt es hier offenbar jedoch keine “vernünftige” Lösung; - und diese funktioniert eben nur bei einer radialen Ausrichtung der Dipolmomente!
Der Lohn dafür, sich mit dieser “Zumutung” des - bislang ungewohnten - physikalischen Denken abzufinden, liegt in der nun offenbar grundsätzlich
überall möglichen sehr präzisen und (bislang mindestens bis zu Si-30 reichenden) lückenlosen Beschreibung aller Atomkerne und ihrer
Eigenschaften - einschließlich der hieraus unmittelbar abzuleitenden chemischen Bindungen - u. v. a. m..
Gute Zahlen, schlechte Zahlen - noch mal: Kernspin und Co.
In der klassischen alten Quantenmechanik gibt es sie schon lange: Die sogenannten guten - und die schlechten Quantenzahlen. Bei der neuen Kernmechanik spielen sie, allem Anschein nach, gleichfalls eine wichtige
Rolle, wobei es in einem etwas abgewandelten Sinne ebenso um deren Belastbarkeit bzw. Zuverlässigkeit geht.
In der Tat sind nämlich die Kernspin-Quantenzahlen - insbesondere für das Kernmechanische Modell - nicht immer gute Quantenzahlen. Ein Beispiel
dafür wurde ja schon mit dem Li-8-Kern weiter oben angeführt, wo ja ganz offensichtlich durch einen gegenüber dem Li-6-Kern fälschlich verdoppelt
angenommenen Kernspin in der Folge nun auch das Li-8-Dipolmoment verdoppelt wurde, obwohl sich kernmechanisch beide Kerne praktisch nicht
voneinander unterscheiden. Da der Kernspin nur von der Kernstruktur und der Nukleonenanordnung im Kern abhängt, ist er kernmechanisch übrigens keine Erhaltungsgröße!
Demnach ist es nun grundsätzlich auch an anderer Stelle möglich, daß ein nicht unmittelbar gemessener, sondern auf Basis einer nicht zutreffenden
Spin-Erhaltung berechneter Kernspin schlicht und einfach falsch sein kann. So besitzen etwa die Natrium-Isotope Na-21 und Na-23, wie erwähnt, nun
jeweils den Kernspin 3/2 und Dipolmomente von 2,39 bzw. 2,21751 MK. Dagegen wird für Al-27 ein Kernspin von 5/2 und ein Dipolmoment von 3,6414 MK angegeben, das kernmechanisch bislang auf eine stärker
deformierte Grundstruktur zurückgeführt wurde.
Vermutlich ist diese Erklärung aber nicht richtig, denn eigentlich sollte der
Kernspin bei Al-27 ebenfalls 3/2 betragen, wodurch sich folglich wiederum ein genau in’s Bild passendes korrigiertes Dipolmoment von 2,1848 MK ergeben würde, welches nun sogar dem gestiegenen Trägheitsmoment in
perfekter Weise Rechnung trägt. Wie gesagt: Das aus dem gleichen Grund schon leicht reduzierte Dipolmoment von Na-21 beträgt 2,39 MK und das von Na-23 - nochmals vermindert - bereits 2,211751 MK.
Auch beim direkt von Mg-23 (0,536 MK) abzuleitenden Magnesium-Nuklid Mg-25 (-0,85512 MK) scheint analog zum vorigen Beispiel gleichfalls eine
Kernspin-Anpassung angebracht, da sich dessen Dipolmoment mit dem (richtigen!) Kernspin von Mg-23, I = 3/2, dann ebenso reduziert auf jetzt sehr plausible 0,5131 MK.
Wenn die vorgenannten Überlegungen stimmen, könnte das natürlich noch weitere Auswirkungen auf das Kernmechanische Modell haben. Da ist es
sicherlich nicht verkehrt, nochmals alle wichtigen Kern-Parameter auf den Prüfstand zu stellen und hierbei als wichtiges Entscheidungskriterium die
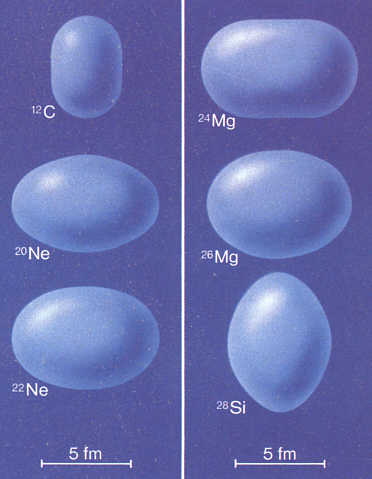
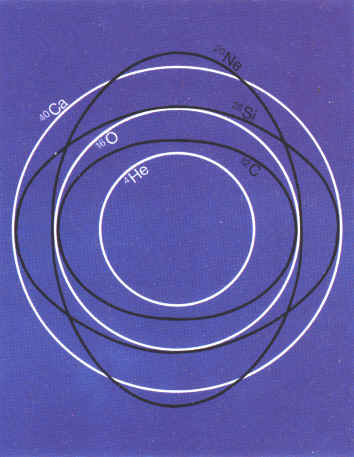
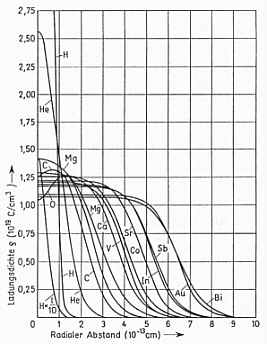
Ladungsdichteverteilung der Atomkerne ebenfalls mit heranzuziehen. In der Abbildung - rechts - sieht man nun, daß beim C-12-Kern die Abnahme der
Ladungsdichte innen zwar nicht so stark ausgeprägt ist wie bei O-16, aber immer noch sehr deutlich. Dies allerdings weckt Zweifel an dem zuletzt favorisierten Kernmechanischen Modell der völligen Spinpaarung, s. o.,
welches hierzu nicht so gut zu passen scheint wie das alte Modell.
Ein wichtiges Indiz für die bei C-12 angenommene zusätzliche Spinpaarung,
aufgrund derer die beiden Li-6-Kernringe nunmehr durch je einen He-6- und einen Be-6-Kernring ersetzt wurden, lag ja u. a. auch in den Dipolmomenten von O-17 und F-17 begründet. Bei F-17 und dem hier angegebenen relativ großen Dipolmoment von 4,722 MK blieb hier - so oder so - demnach nur
eine Lösung übrig, wonach in einem (bei O-17 völlig spingepaarten) He-6-Kernring ein Neutron durch ein Proton ersetzt wurde, woraus dann bereits 4,707 MK dieses Dipolmoments resultierten...
Tatsächlich läßt sich beim O-17-Nuklid mit (gegenüber der Grundstruktur) um 60° verdrehten Symmetrieachse des He-6-Kernringes aus eben dieser
Symmetrieabweichung - zweimal stehen sich nun jeweils ein Proton und ein Neutron gegenüber - sowie dem zentralen ungepaarten Neutron nunmehr der korrekte Kernspin I = 5/2 ableiten (altes Modell - ohne zusätzliche
Spinpaarung). Ganz ähnlich sieht es ebenfalls beim “Spiegelkern” F-17 aus, wo die asymmetrische Konfiguration des ursprünglichen He-6-Kernrings
natürlich nicht dadurch aufgehoben wird, daß jetzt hier ein Neutron durch ein Proton ersetzt wurde.
Die aus alledem zu ziehende richtige Lehre ist demnach also nicht, daß eine Spinpaarung gegenüberliegender Nukleonen folglich etwa auch bei den
6er-Kernringen von C-12 energetisch begünstigt wäre, sondern vielmehr nur, daß von 6-er-Kernringen umschlossene Nukleonen stets Neutronen sein
müssen (bzw. nur als solche stabil sind)! Die ominöse Spinpaarungsenergie ist also wirklich nur die banale Folge der banalen alternierenden Anordnung der Protonen und Neutronen in den Kernringen. 
Das C-12-Nuklid
Alles magisch - oder was?
Wenn es nun also wahr ist, daß sowohl die Spinpaarung als auch die “magische” Doppelbesetzung von Nukleonen-Orbitalen jeweils zu einer
Steigerung der Bindungsenergie führen - wann kommt es dann zum einen und wann zum anderen?
Eine Spinpaarung, welche durch den antiparallelen Kernspin von in einem
Kernring gegenüberliegenden gleichartigen Nukleonen - Protonen oder Neutronen - entsteht, gibt es in perfekter Weise bei den (auch als
Alpha-Teilchen bekannten) Helium-4-Kernen, zum Teil aber bereits bei Tritium bzw. Helium-3, wo sich einmal zwei Neutronen und einmal zwei Protonen - eben auf Grund ihres antiparallelen Spins - weitgehend
problemlos gegenseitig durchdringen können. - Da dies jedoch bei einem Li-6-Ring naturgemäß nicht geht, ist ein einzelner Li-6-Ring demnach
übrigens nicht stabil, sondern erst gemeinsam, verschränkt mit einem zweiten - als das gerade zuvor beschriebene C-12-Nuklid.
Ebenfalls instabil ist - für sich allein genommen - aber auch ein He-4-Kern mit zusätzlich (paarweise) doppelt besetzten Kern-Orbitalen: Für He-6
beträgt die Halbwertszeit demnach 0,8 Sekunden, während für Be-8 nur eine Zustandsbreite von 6,8 eV gemessen wurde. Erst in Verbindung mit einer
stabilisierenden Deuterium-Achse entsteht nicht nur aus dem He-4-Kern eine neue, stabile Li-6-”Verbundstruktur”, sondern analog dazu etwa aus
He-6 ebenso der stabile Verbundkern Be-9 - mit noch zusätzlich einem doppelt besetzten Protonen-Orbital auf der Deuterium-Achse.
Genauso aber, wie der He-4-Kern ein Musterbeispiel für die Spinpaarung
ist, verhält es sich danach beim “magischen” O-16-Kern bezüglich der hier - nunmehr komplett - doppelt besetzten Kern-Orbitale! Eben dieser magische
O-16-Kernring sollte, gemeinsam mit zwei dort aufgereihten Li-6-Kernringen, in der Folge auch das Grundgerüst für den sich gleichfalls durch seine hohe
Bindungsenergie auszeichnenden Si-28-Kern bilden. - Man kann sich nun allerdings fragen, ob nicht ein einziger 6er-Kernring mit doppelt besetzten
Orbitalen, da offenbar ebenfalls stabil, nicht energetisch noch günstiger sein sollte, als die genannten Li-6-Ringe? -
Die seinerzeit in Karlsruhe für Si-28 ermittelte Kernform würde diese These zunächst stützen. Problematischer ist es allerdings bei einigen anderen
Kernen, - weniger, was deren Quadrupolmoment, sondern die absoluten Abmessungen anbelangt. Dabei muß jedoch berücksichtigt werden, daß die
äußeren Dimensionen von C-12 und Si-28 systematisch etwas zu klein ausgefallen sind, da hier fälschlich von einem negativen Quadrupolmoment ausgegangen wurde. So gesehen paßte es durchaus zum ermittelten
Quadrupolmoment, in Mg-24 ein verdoppeltes C-12-Nuklid mit doppelt besetzten Kern-Orbitalen zu sehen - oder in Ne-20(-22) ein gleichermaßen
verdoppeltes B-10(-11). Im letzten Fall könnten Kernspin und Dipolmoment jedoch nicht Null sein; - wohl aber dann, wenn wiederum C-12 auch für die
genannten Neon-Nuklide - mit entsprechend doppelt besetzten Orbitalen - die Grundlage darstellte!
Ganz besonders einsichtig und auf Grund der maximalen Bindungsenergie plausibel wäre es dann aber, wenn das - für sich genommen - schon absolut
magische Fe-56-Nuklid nunmehr zusätzlich zur O-16-Grundstruktur über vier dort aufgereihte “verdoppelte” (doppelt besetzte) 5er-Ringe (3x He-5 und 1x
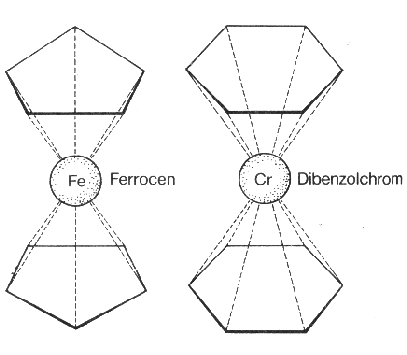
Li-5) verfügte. Für Cr-52 müßte man demgegenüber von drei auf dieser Grundstruktur aufgereihten verdoppelten 6er-Ringen (He-6 und 2x Li-6) ausgehen, wofür auch die selbstähnliche Struktur von Dibenzolchrom - mit
zwei sechseckigen Benzolgruppen - spricht, während wiederum Eisen eine “Ferrocen”-Verbindung mit dem fünfeckigen Cyclopentadien bildet.
Die im Vergleich zu ihren geradzahligen Nachbarn jeweils besonders hohen Bindungsenergien von S-34 und Ar-38 können jetzt allerdings nicht durch die
(bei dem auf Be-8 basierenden O-16 oder dem auf C-12 basierenden O-18 nicht mögliche) jeweilige Verdoppelung der Kernstrukturen von O-17- und
F-19 erklärt werden - zumindest im Grundzustand - (da Dipolmoment und Spin dann nicht Null wären). Beide basieren vielmehr auf der obigen (teilweise modifizierten und) erweiterten Ne-20-Kernstruktur.
Angeregte Kernzustände? - Unterschiedliche Kernstrukturen!
Bereits im Grundsatzbeitrag “Realistisches Kernmechanisches Modell” wurde schon frühzeitig der (zunächst eher noch unzureichende!) Versuch
unternommen, die sogenanten angeregten Kernzustände - entgegen der üblichen Anschauung - als unterschiedliche Kernstrukturen zu interpretieren.
Aber nur beim frühen “Paradebeispiel” für die hier sehr überzeugende Zuordnung der richtigen Kernspin-Quantenzahlen erweist sich das dort
angegebene Modell von B-10 grundsätzlich auch weiterhin als das - in diesem Fall - womöglich zutreffende. Ganz besonders schwierig und immer
abhängig vom jeweiligen Stand der Modelldiskussion - in der Regel eher unzutreffend - waren demgenüber die Angaben zum C-12-Nuklid.
Inzwischen ist (s. o.) jedoch klar, daß C-12 im Grundzustand aus zwei Li-6-Kernringen, mit jeweils alternierenden Protonen und Neutronen, besteht
(wobei sich zwei Neutronen aus energetischen Gründen dann ganz innen befinden). Das in der Fig. 4 angegebene Modell für die weiteren angeregten
Zustände ist aber - obwohl der Kernspin stimmte - gleich aus mehrerlei Gründen falsch. Zum einen gibt es hier, anders als beim Modell von B-10,
bei C-12 keine geometrisch bedingten “Rastsstellungen”. Zum anderen sind die ermittelten Differenzen der Energieniveaus, gerade auch im Vergleich zu
B-10, viel zu groß, um derartige Annahmen zu stützen. - In Folge der bisherigen Modelldiskussion stehen aber bereits gut geeignete
Alternativ-Strukturen zur Verfügung, um die in Frage stehenden Niveaus in jeder Beziehung adäquat zu besetzen:
Wenn nämlich Li-8, s. o., (mit zwei doppelt besetzten Neutronen-Orbitalen der Li-6-Grundstruktur) den Kernspin 2+ aufweist, sollte dies ebenfalls für
den ersten angeregten Zustand von C-12 gelten - wo in gleicher Weise sogar alle Orbitale doppelt besetzt sind - oder für den zweiten angeregten Zustand von C-12 mit Spin 0+ und einen ebensolchen Li-6- Basis-Kerning. -
Einfach ist die Kernstruktur-Analyse beim Li-6-Nuklid selber und dessen ersten angeregten Zuständen: Im Grundzustand findet man zunächst He-4 plus Deuterium, danach einen komplementär zusammengedrückten (3+)
und weiter einen nicht deformierten Li-6-Kernring (0+).
Sehr hilfreich ist die richtige Zuordnung der beobachteten Kernspin-Zahlen
zu den in Frage stehenden Kernstrukturen auch bei Mg-24. Im Grundzustand findet man 0+, dann 2+, 4+ und danach nochmal 2+. Da der Kernspin 0+ nur
einmal vorkommt, bleibt in der Tat nur eine mögliche Schlußfolgerung übrig: Dieser Kernspin korrespondiert im Grundzustand mit der “verdoppelten”
C-12-Struktur (alle Kernring-Orbitale sind nun doppelt besetzt). Jedoch ist die - auf Grund der gemessenen zylindrischen Kernform - lange favorisierte Struktur aus drei 8er-Kernringen so fragil, wie man das eigentlich vermuten
sollte und existiert an dieser Stelle wohl überhaupt nicht. Dagegen führt etwa ein um ein halbes Nukleon aus der Symmetrieachse verdrehter mittlerer
8er-Kernring gegebenenfalls auch schon mal zum Kernspin 4+!
Wenn aber ein durchweg doppelt besetzter “magischer” Kernring bezüglich
der Bindungsenergie dermaßen stark begünstigt wird, dann sollte dies in gleicher Weise ebenfalls für den unmittelbar voraufgehenden Kern gelten, also etwa für N-15 (O-16 minus ein Proton). Dies erklärte zugleich den hier
auffällig kleinen Einfangquerschnitt für Neutronen - da ja nur noch ein einfach besetztes Protonen-Orbital übrig ist.
So dies alles wirklich zutrifft, müßte die Ladungsdichteverteilung von N-15 in etwa der von O-16 gleichen. Bei den Kernmechanischen Elektronen-Orbitalen von N-14 und N-15 hingegen müßten sich wie bei O-16
und O-18 ebenfalls meßbare Abweichungen zeigen. Deshalb könnte N-15 (anders als N-14) analog zu O-16 dann wahrscheinlich auch besondere supraleitende Eigenschaften besitzen. -
Da für C-14 und N-14 demnach von unterschiedlichen Modellen auszugehen ist, wo sich nun die das Dipolmoment bestimmenden (einfach bzw. doppelt
besetzten) Nukleonenorbitale jeweils in einem Kernring gegenüber stehen, kann jetzt endlich - und engültig - die zuletzt falsche radiale Orientierung der
Dipolmomente zu den Kernringen korrigiert werden: D. h., die ursprünglich angenommene tangentiale Ausrichtung ist doch die richtige; Kernspin und
Dipolmoment sind parallel orientiert! Wie sich zeigt, ist auch die Anpassung des B-10-Kernmodells kein Problem, während das - nicht stabile - Be-10-Nuklid (mit dem Kernspin 0) dann eben etwa aus einem
Be-8-Kernring und einem mit diesem verschränkten He-4-Kernring besteht.
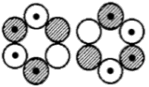
Der Beweis - ein besonderes Kernmechanisches Modell im Detail
Schon mehrfach wurde auf ein auffälliges Kernmechanisches Modell hingewiesen, welches im wesentlichen aus zwei zu einer liegenden Acht
verschmolzenen Li-6-Kernringen aufgebaut ist.
Mit einem (beiden Ringen gemeinsamen) mittleren Neutron und einem dieses umschließenden weiteren 6er-Kernring, Be-6- bzw. Li-6, führt die
C-11-Struktur im ersten Fall zu O-17 (mit dem Dipolmoment -1,89370 MK und einem negativen Quadrupolmoment), bzw. zu F-17, wo zum besagten
Dipolmoment (auf Grund des fehlenden Neutrons) nun noch 4,706 MK vektoriell im Winkel von, nicht genau, 90° hinzu zu addieren sind - der
teilweise spinkompensierte Li-6-Ring steht etwas schräg! -, weshalb das resultierende Dipolmoment von 4,722 MK um mindestens 3,7 % kleiner erscheint, als das für 90° berechnete.
Wesentlich überzeugender fällt das Ergebnis jedoch aus, wenn das weiter oben auf dieser Seite angesprochene Modell mit einer komplementären
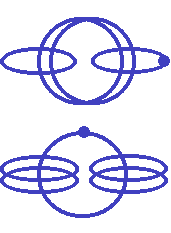
B-11-Struktur jetzt im Detail analysiert wird. Dabei zeigt sich nämlich, daß zum F-19-Nuklid nicht, wie oben vermutet, zwei “spingepaarte Protonen”
zugefügt werden, um zu Na-21 zu gelangen, sondern daß sich die doppelt besetzten Protonen-Orbitale vielmehr in der B-11-Grundstruktur diagonal gegenüber stehen und daß dies haargenau zum richtigen Ergebnis führt -
falls man direkt vom Dipolmoment von F-19 ausgeht. Wenn dann bei Na-23 wirklich noch zwei “spingepaarte Neutronen” beim zentralen Be-8-Ring dazu
kommen, führt das lediglich zu einer Dehnung der B-11-Struktur und damit zu einer kleinen Dipolmoment-Reduzierung von weniger als 0,2 MK. Ganz
ähnlich verhält es sich bei Na-22 (sowie Na-24), wo ganz außen in der B-11-Struktur jeweils noch ein doppelt besetztes Neutronen-Orbital hinzu
kommt und deren Dipolmoment um 0,7 MK reduziert und wiederum exakt zum richtigen Dipolmoment führt.
Nicht so einfach ist die KM-Strukturanalyse bei Al-27. In der Tabelle der Kernmodelle wurde das Al-27-Nuklid ja ebenfalls der F-19-Grundstruktur
zugeordnet; wobei außerdem noch erwartet wurde, daß alle Orbitale des mittleren Be-8-Kernringes doppelt (mit jeweils 4x 2 Protonen und 4x 2 Neutronen) besetzt sein sollten. - Auch wenn dieses Bild nun auf 4x 2 Neutronen im genannten Kernring korrigiert wird - und die 4x 2 Protonen auf
die gerade beschriebene “liegende Acht” übertragen werden, stimmt das so erhaltene Ergebnis von 2,193 MK (4x cos 60°x 0,3 Mk = 0,6 MK werden von
den 2,793 MK - auf Grund des fehlenden zentralen Protons - abgezogen) noch immer nicht mit den Meßdaten, 3,64140 MK beim Kernspin 5/2+, überein.
Kernmodell von Al-27
Anders sieht es aus, wenn der Kernspin tatsächlich 3/2+ ist und nicht 5/2+!
Das führt nach der Rechnung 3/5 x 3,6410 zum hervorragend passenden (korrigierten) neuen Meßwert 2,18484 MK. Im Prinzip ähnlich scheinen die
Verhältnisse bei Mg-23 (0,5131 MK) und Mg-25 (-0,85512 MK), da 3/5 x 0,855 MK nämlich wieder genau 0,513 MK ergibt, oder: Das (um einen Li-6-Ring) erweiterte Si-29-Kernmodell führt beim korrigierten Spin 5/2+
zum dito Meßwert -2,776 MK, die Modellrechnung zu 2,793 Mk. Bei P-31, 1/2+, 1,13166 MK, (mit “magischem” O-16 Kernring und einem Neutron
mehr als bei Na-24) ergibt die Modellrechnung sodann 1,21 MK.
Für Al-25 und Al-27 gibt es aber im Modell noch eine rotationssymmetrische Variante, die beim originären Kernspin 5/2 jeweils zu einem Dipolmoment
von 3,632 MK führt (siehe Tafel). Ebenso können die auf B-11 folgenden Nuklide B-13, 15 und 17 erklärt werden oder auch Li-7, 9 und 11 durch eine
abgespeckte Miniform in der Art eines “EI- bzw. M”-(Trafo)kerns. - Für die Kernmechanik und gegen die Quantenmechanik spricht schon jetzt die
bemerkenswert gute Übereinstimmung von Modell und Wirklichkeit.
Gerd Schulte
|




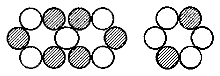 O-17, 5/2+, -1,8937 (-1,913) MK
O-17, 5/2+, -1,8937 (-1,913) MK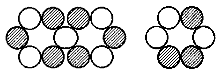 F-17, 5/2+, 4,722 (5,073) MK
F-17, 5/2+, 4,722 (5,073) MK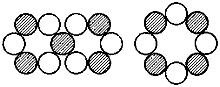 F-19, 1/2+, 2,6287 (2,793) MK
F-19, 1/2+, 2,6287 (2,793) MK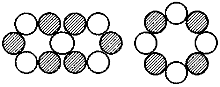 Ne-19, 1/2+, -1,886 (-1,913) MK
Ne-19, 1/2+, -1,886 (-1,913) MK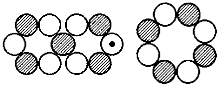 F-20, 2+, 2,092 (2,093) MK
F-20, 2+, 2,092 (2,093) MK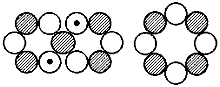 F-21, 5/2+, 3,93 (3,697) MK
F-21, 5/2+, 3,93 (3,697) MK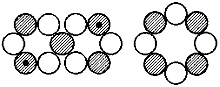 Na-21, 3/2+, 2,390 (2,386) MK
Na-21, 3/2+, 2,390 (2,386) MK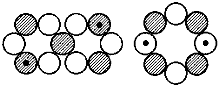 Na-23, 3/2+, 2,2175 (2,386) MK
Na-23, 3/2+, 2,2175 (2,386) MK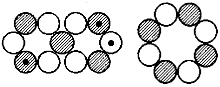 Na-22, 3+, 1,746 (1,71) MK
Na-22, 3+, 1,746 (1,71) MK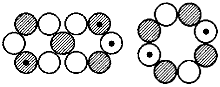 Na-24, 4+, 1,68 (1,71) MK
Na-24, 4+, 1,68 (1,71) MK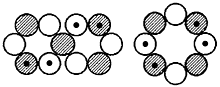 Al-27, 5/2+, 3,6414 (3,632) MK
Al-27, 5/2+, 3,6414 (3,632) MK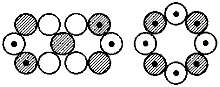 P-31, 1/2+, 1,13166 (1,21) MK
P-31, 1/2+, 1,13166 (1,21) MK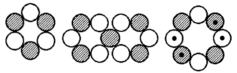 Si-29, 5/2+*, 2,776 (2,793) MK
Si-29, 5/2+*, 2,776 (2,793) MK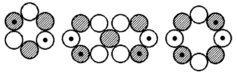 Cl-35, 3/2+, 0,82183 (0,91) MK
Cl-35, 3/2+, 0,82183 (0,91) MK 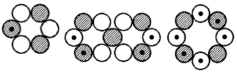 Cl-36, 2+, 1,28538 (1,393) MK
Cl-36, 2+, 1,28538 (1,393) MK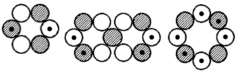 Cl-37, 3/2+, 0,6841 (0,693) MK
Cl-37, 3/2+, 0,6841 (0,693) MK












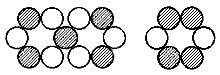 F-17’, 3/2+*, 2,8332 (2,793) MK
F-17’, 3/2+*, 2,8332 (2,793) MK