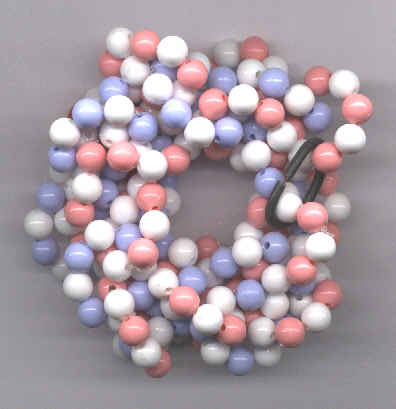|
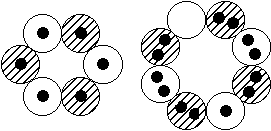
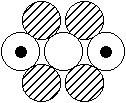
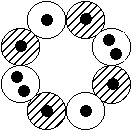
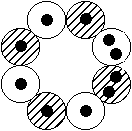
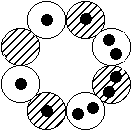
Kernstrukturen, Kernspin und Dipolmomente
Falls nach Betrachtung der obigen Kernmodelle der Eindruck entstanden sein sollte, daß die Kernmechanischen Modellstrukturen damit erschöpft
wären, so stimmt dies natürlich nicht; -
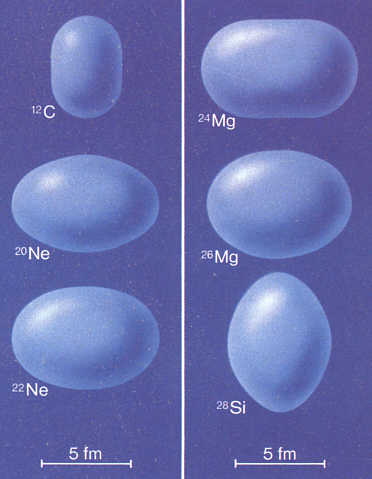
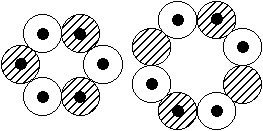
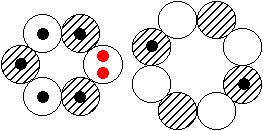
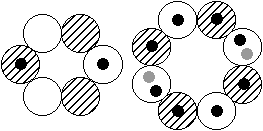
nicht einmal für Magnesium. Dort gibt es nämlich bei den gg-Kernen Mg-24 und Mg-26 angeregte Zustände, jeweils mit I = 2+ und µ = 1,0 MK, die ebenso im Rahmen dieses Modells erklärt werden können. Der einzige Unterschied zwischen beiden Kernen liegt darin, daß bei Mg-26 der 8er-Ring mit gegenüberliegenden doppelten (statt einfachen) Neutronen-Orbitalen bestückt ist. Bei Si-28, mit I = 2+, gibt es dito ein doppeltes Neutronen-Orbital, bei-Si-27 dazu
zwei Dreifach- Protonen-Orbitale, bei Ar-33 zwei Dreifach-Neutronen-Orbitale.
Si-28, 2+, +1,1 (<1,25) MK
Ar-33, 1/2+, -0,723 (-0,7) MK
Die Schwefel-Isotope S-33, -34 und -35 sind aber, wie auch Ar-36...40 (nach einem eigentlich
unnötigen Umweg) erst dann - quasi “sudokumäßig” - zu ermitteln, wenn man dem Ganzen das richtige Kernmodell zu Grunde legt. Das in diesem Fall richtige Modell ist jenes, aus vier 8er-Kernringen
bestehende (je zwei paarweise gebündelt), das wiederum eine selbstähnliche makroskopische Entsprechung in der charakteristischen S-8-Molekel hat. - Spätestens im Perlenmodell erkennt man außerdem,
daß das am Ende des Optimierten Modells zuerst angenommene Kernmodell mit einem zentralen 8er-Ring und vier dort aufgereihten
6er-Ringen, allen etwaigen Hilfsannahmen zum Trotz, nicht funktionieren kann. -
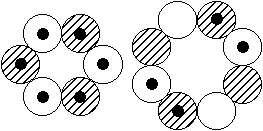
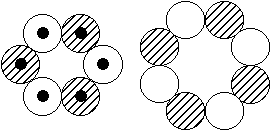
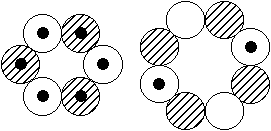
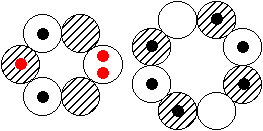
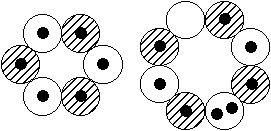
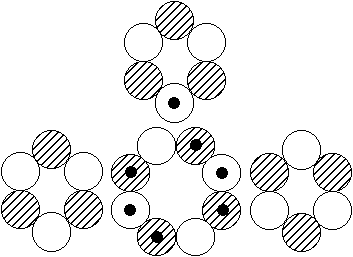
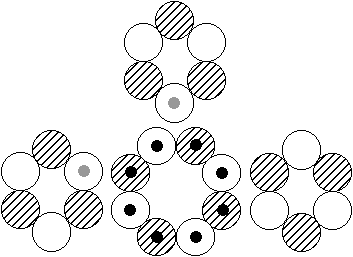
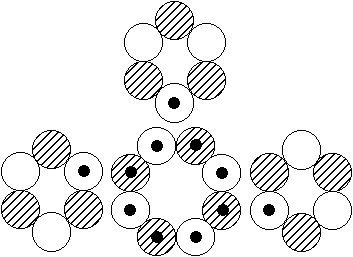
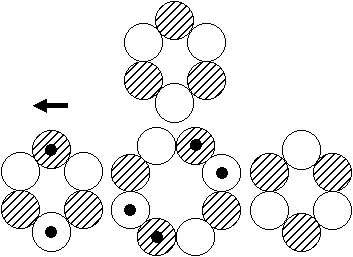
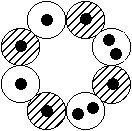
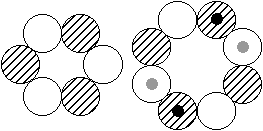
Existiert dann wenigstens das Kernmodell mit dem zentralen 8er-Ring und den drei 6er-Ringen, wie es die Abbildung rechts suggeriert? - Das so
beschriebene, sehr plausibel scheinende Modell gibt es offenbar wirklich. Seine Spuren findet man nämlich nicht nur jeweils als (erste, zweite oder dritte) angeregte Zustände mit I = 0 bei sehr geringen Anregungsenergien
im Termschema des Basis-Nuklids 13-Al-26, sondern dito bei Al-28, P-30 und P-32 (2 oder 4 doppelt besetzte Protonen-Orbitale, bzw. zusätzlich 2
Neutronen-Orbitale). Aber auch Cl-33 mit I = 3/2+ und µ = 0,752 MK sowie vermutlich auch 19-K-41 und viele weitere Kerne basieren offenbar auf der genannten Al-26-Grundstruktur.
Cl-33, 3/2+, +0752 MK
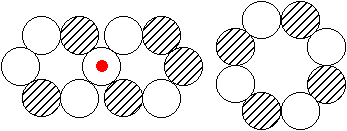
Bei Schwefel, S-32, führt dagegen nach längerer Überprüfung alternativer Strukturen letztlich doch kein Weg vorbei (Abb. r.) am ursprünglichen
4x8-Kernringmodell!
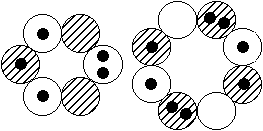
Doch zurück zum Chlor und den nun folgenden stabileren und wichtigeren Isotopen: Bei Cl-34, wo Kernspin und Dipolmoment jeweils Null sind, sind
hier demnach alle Orbitale des großen, mittleren Kernrings doppelt besetzt, - was unmittelbar einleuchtend erscheint.
Cl-34, 0+
Cl-35, 3/2+, +0,82187 (0,7) MK Cl-36, 2+, +1,28547 (1,2934) MK
Bei Cl- 35, - 36 und -37 werden anschließend nacheinander jeweils die inneren Neutronen-Orbitale der drei Li-6-Kernringe (doppelt) aufgefüllt. In
der Abbildung rechts kann man sehen, daß die Spin-Achsen der Orbitale, bzw. die Vektoren der Dipolmomente bei Cl-36 einen Winkel von ca. 45°
zueinander aufweisen, was rechnerisch zu einem hieraus resultierenden Dipolmoment von insgesamt 1,2934 MK (Messung 1,2855 MK) führt.
Cl-37, 3/2+, +0,684 (0,7) MK
Die folgenden Isotope gehen also beim Chlor (Z = 17) auf jeweils nur eine Grundstruktur zurück. Die chemischen Eigenschaften sind
hier sowieso gleich. - Das ist aber nicht bei jedem Element automatisch der Fall, insbesondere dann nicht, wenn die Grundstruktur eben nicht für alle Isotope die gleiche ist! -
Bei C-13 und -14 gegenüber (dem mit ca. 99% dominierenden) C-12 ist das so - und wohl auch bei S-33-36, gegenüber dem mit ca. 95% weitaus
häufigeren S-32-Nuklid. Auf die auffällige Korrelation zwischen Kernstruktur und S-8-Molekel wurde ja schon hingewiesen; was aber, wenn die für S-32
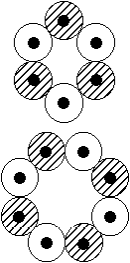
gefundene Doppelsandwich-Struktur für die folgenden Schwefel-Isotope nicht in Frage kommt, wie das schon bei S-34 mit I = 2+ und µ = 1,0 MK, Abb. rechts oben, der Fall ist?!
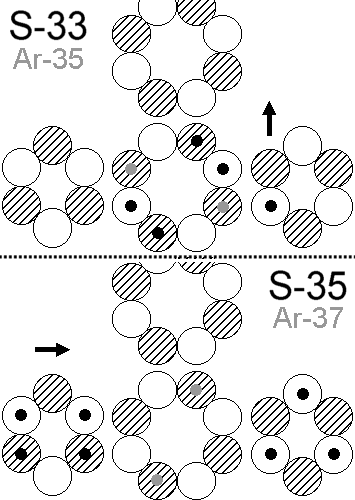
Für S-35 ist die Frage aber zunächst gar nicht so leicht zu beantworten, zumal auch das neue, bei den verschiedenen Chlor-Isotopen und S-34
angewendete Kernmechanische Modell für S-35 mit I = 3/2+ und wiederum µ = 1,0 KM (!) einfach nicht passen will. - Wenn das Kernmechanische
Modell - wie bislang überall sonst - aber richtig ist, muß es auch hier eine Lösung geben... und die gibt es tatsächlich. Man muß nur eine offenbar
bestehende psychologische Sperre überwinden und den mittleren (obigen) 6er-Kernring durch einen 8er-Kernring ersetzen - und schon stimmt alles:
Bei S-35 ist nun bei einem der verbliebenen zwei 6er-Kernringe, anders als bei S-34, nicht nur ein Protonen- und Neutronen-Orbital doppelt besetzt,
sondern es sind hier jeweils zwei! - was aber exakt zum gleichen Ergebnis führt: µ = 1,0 MK in Längsrichtung des Kerns und einem Quadrupolmoment
von ebenfalls ca. +0,05 b. Bei S-33 (Abb. R-oben), I = 3/2+ und µ = 0,64 MK senkrecht dazu ist dieses mit -0,064 b wie erwartet negativ.
Im Zuge weiterer Überlegungen rückt danach noch eine früher propagierte, (dann aber wegen der exotischen Kernform wieder beiseite gelegte, weil
zu künstlich anmutende?!) Konfiguration aus einem 10er-Kernring und fünf dort aufgereihten 6er-Ringen wieder in den Blickpunkt des Interesses.
Dabei paßt gerade die Sonderstellung dieses Kerns, im Vergleich zu seiner unmittelbaren Nachbarschaft, bestens zu seinen magischen Eigenschaften und dem Schalenmodell, mit dem wirksamen Abschluß der
Kernschale genau an dieser Stelle. Die gleiche auffällige Sonderstellung bei der Bindungsenergie konnte übrigens ja auch schon beim Kernmechanischen Modell von O-16 konstatiert werden.
Wenn die vorstehenden Überlegungen richtig sind, muß es natürlich Spuren
geben, die das bestätigen; - und die Spuren gibt es tatsächlich: Wenn alle fünf Orbitale des 10er-Kernrings doppelt besetzt werden, führt das zu
25-Mn-50 - mit I = 0+ im Grundzustand. Wenn dazu alle Orbitale von zwei 6er-Ringen verdoppelt sind, ergibt das 31-Ga-62, ebenfalls mit I = 0+ im
Grundzustand. Bei dito vier doppelt besetzten Li-6-Ringen, also dem Nuklid 37-Rb-74, ist das Resultat das gleiche. Wenn ausschließlich die Orbitale
der äußeren fünf 6er-Ringe verdoppelt werden, führt das nunmehr zu 35-Br-70. Auch der Grundzustand dieses Nuklids lautet I = 0+.
Besonders interessant sind hier alle Kerne, die mindestens einen 6er-, bzw. 10er-Kernring enthalten, wobei nun alle Ringorbitale eines solchen
Kernrings jeweils komplett gleich mit einem, zwei oder drei Protonen und / oder einem, zwei oder drei Neutronen besetzt sind. Rein rechnerisch
kommen demnach Kernstrukturen mit folgenden Kernring-Konfigurationen für eine genauere Überprüfung in Frage: 6 + 6 / 8 + 6 / 8 + 6 + 6 / 8 + 6 + 6
+ 6 / 10 + 5x 6, usw., usw.. Tatsächlich findet man dort praktisch überall entsprechende Kernzustände mit I = 0!
Um aber nochmals auf den Zusammenhang zwischen Kernformen und Kernstrukturen zurückzukommen: gerade wurde in den USA eine neue
Studie veröffentlicht, bei welcher verschiedene leichte Atomkerne mit hochenergetischen Elektronen beschossen wurden. Gegenüber dem oben geschilderten Versuchsaufbau im Kernforschungszentrum Karlsruhe, wo
seinerzeit Elektronen-Energien von 104 MeV eingesetzt wurden, konnte nunmehr die Energie des Target-Strahls mit 5,8 GeV um mehr als das fünfzigfache gesteigert werden. John Arrington und andere vom Argonne
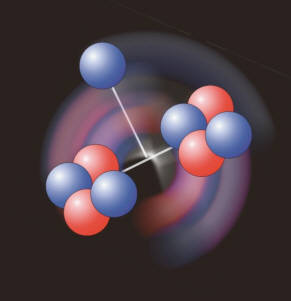
National Laboratory in Illinois berichten in den Physical Review Letters, Ausgabe vom 13. 11. 2009, was sie dabei gefunden haben: Demnach besteht etwa der Kern von Be-9 im wesentlichen aus zwei He-4-Clustern
und einem relativ lose gebundenen zusätzlichen Neutron. Genau dies hat aber das Kernmechanische Optimierte Modell bereits fünf Jahre zuvor (am 24. 11. 2004) postuliert.
Vom magischen Kern O-16 zu O-18 und F-18 ist es dann aber kein großer
Schritt mehr: Im Grundzustand sind zwei bei O-16 doppelt mit Neutronen besetzte, gegenüber liegende Kernring-Orbitale nunmehr eben gleich mit
drei Neutronen besetzt. Das ändert weder etwas am Kernspin, noch am Dipolmoment, die beide jeweils Null sind. Bei dem angeregten Zustand mit
dem Spin 1-, wo die beiden Dreifach-Orbitale etwa im Winkel von 90° angeordnet sind, ergibt sich rechnerisch ein resultierendes Dipolmoment
von ca. 0,785 MK (Absolutwert). Bei dem niedriger liegenden Zustand 2+, mit gemessenen -0,57 MK, ist dann offenbar auch das sich zwischen
beiden befindende Protonen-Orbital dreifach besetzt (- und das gegenüber liegende folglich nur einfach). Rechnerisch ergibt dies zunächst (-)0,75 MK,
mit einer plausiblen Winkelkorrektur der Neutronen-Orbitale von 43° (links) und 47° (rechts), statt 45°; bei symmetrischer Anordnung, O-16, auch der
doppelt besetzten Protonen-Orbitale von 90 auf 89° stimmt das Resultat dann aber genau.
Bei dem isobaren Nuklid F-18 mit dem Kernspin 1+ sollte das Ergebnis von rechnerisch 0,93 MK (Absolutwert) bereits ohne Korrektur annähernd
richtig sein; - falls der Grundzustand aber 0+ wäre, Abb. rechts, müßte das Dipolmoment natürlich ebenfalls Null sein!
Ganz lange Kernringkette - oder die Kraft, die durch den Knoten geht
Ganz gewöhnliche 8er-Kernringe aus zunächst jeweils 4 Protonen und 4 Neutronen lassen sich relativ problemlos auch zu einer langen Kette
zusammenfügen. Stabil ist eine solche Kernring-Kette wiederum aber nur dann, wenn sie auch mechanisch stabil, d. h. zunächst einmal in sich
geschlossen ist. 8x8 Kernringe ergeben so etwa das Nuklid Zn-64. Dabei sieht man jedoch bereits, daß sich hier offenbar schon zwei “fest
eingepackte” innere Protonen in an dieser Stelle energetisch günstigere Neutronen umgewandelt haben. Bei entsprechend dichterer Kernpackung
passiert dies später zunehmend häufiger. Einzige Ausnahme: Wenn eine bestimmte Kernring-Konfiguration ausgereizt ist und noch keine alternative
neue zur Verfügung steht, wird der Aufbau wieder lockerer und es werden zusätzlich nur noch neue Protonen eingebaut, siehe: “Magische Zahlen”!
Die wirksame Stabilisierung einer längeren Kernring-Kette kann insbesondere durch Knoten in der Kette und (mehrfache) Umschlingungen
bewirkt werden. Ist dies jedoch an einer Stelle - so oder so - nicht möglich, tritt nun der charakteristische Backbending-Effekt auf, der auf Grund der
plötzlichen Zunahme des Trägheitsmoments bei starker Eigenrotation (wegen des Auseinanderziehens der locker zusammengerollten Kette) durch starke Fliehkräfte bewirkt wird.
Eine besonders feste und zusäztlich besonders elastische “Kranzstruktur” gibt es sodann beim Blei, mit einer mehrfach gewickelten und gewendelten Kernringkette, die sich tatsächlich auch nicht so einfach spalten läßt.
Ganz anders sieht es aber aus, wenn die aus 29 Kerenringen bestehende Kernringkette ab Thorium-232 gerade nur durch zwei eingewirkte Knoten,
d. h. einen Doppelknoten stabilisiert werden kann. Egal ob Kreuzknoten oder Altweiberknoten: Beide Einzelknoten-Cluster werden jeweils nur durch
zwei Kettenglieder zusammengehalten und können demzufolge leicht durch eingefangene thermische Neutronen gespalten werden. Gerade das ist aber die Grundlage der Kernspaltung. Es ist dies also auch die Kraft, die -
eben nur(!) - durch den Knoten geht.
Auf Grund neuer Experimente lohnt es sich aber, nochmals auf die zuvor erwähnte, nur schwer spaltbare Kernmechanische Kranzstruktur zurück zu
kommen: Beim mit über 50 % häufigsten - doppelt magischen - Bleiisotop Pb-208 ist die gesamte Kernringkette gegenüber (dem Reinelement)
Th-232 um drei Kettenglieder à acht Nukleonen kürzer. Kernmechanisch also nicht verwunderlich, daß Pb-208 gegenüber seinen Nachbarn - mit
mehr oder weniger Neutronen - demzufolge auch besonders stabil ist, bzw. die Anregungsenergie für den ersten angeregten Zustand hier ebenfalls
besonders hoch ist, s. a. einschlägige Abbildungen zu den “magischen Kernschalen”.
Bei der gleichen - nunmehr extrem eng gewickelten - Kranzstruktur geht es aber noch etwas knapper: etwa um ein weiteres Kettenglied (mit wiederum
acht Nukleonen) weniger. Dieses führt zum besonders kompakten Kern Hg-200, der sich, Kernmechanisch kaum überraschend, noch ziemlich
ähnlich verhält wie das gerade beschriebene Pb-208 - aber (abhängig von der jeweiligen Kernstruktur) viele leichtere Quecksilberisotope eben nicht!
Man brauchte demnach also nur die wichtigsten relevanten Kernparameter, insbesondere das Yukawa-Potential, Kernmechanisch möglichst exakt zu modellieren, um die Ergebnisse bei bestimmten Kernspaltungen - etwa die
nunmehr gefundenen sehr unsymmetrischen Spaltprodukte bei Hg-180 (mit einer mechanisch extrem instabilen “schlabbrigen” Kernringkette) - auch in schwierigeren Fällen richtig vorauszusagen. Für die Kernmechanik ist dies
beim vorliegenden CERN-Experiment noch eine leichtere Übung; - nicht so
aber für das mathematisch eher simpel gestrickte Schalenmodell.
Wichtige Spaltfragmente - mehr als nur Knoten in der Kette
Daß die Kernspaltung genau mit einer (durch Doppelknoten stabilisierten) Kernringkette aus 29 Kettengliedern a 8 Nukleonen korrespondiert und bei
Thorium-232 beginnt, könnte ja vielleicht noch ein seltsamer Zufall sein, aber richtig interessant und (kernmechanisch ja eigentlich wieder nicht!)
erstaunlich wird es bei den hieraus resultierenden Spaltfragmenten. Bekanntlich ist die Massenverteilung der Spaltprodukte bei Thorium, Uran, Plutonium und auch Californium sehr asymmetrisch.
Kernmechanisch ist das jedoch überhaupt nicht verwunderlich, weil nach dem Reißen der Kernringkette an der “Sollbruchstelle” beim Einfang relativ
langsamer, thermischer Neutronen aus dem bisherigen Doppelknoten nun bevorzugt ein einfacher Knoten hervorgeht. Damit dieser nun wieder stabil
geschlossen werden kann, muß die Kette nun etwa mindestens 17 Glieder lang sein - was z. B. mit Cäsium-136/-137, bzw. Barium-136/-137 korrespondiert. Mit größerer Zugspannung ist aber ggf. auch noch eine
geschlossene Kernringkette aus 16 Kettengliedern möglich. 8x 16 führt dann wiederum zu A=128 und Jod-128-133 bzw. Xenon-128-136 usw...
Alternativ kommt an dieser Stelle außerdem ein Kernmodell in Frage, das aus zwei ineinander gefügten, geschlossenen Zn-64-Kernringketten
besteht. Dabei ist aber immer zu berücksichtigen, daß die Kernladung (durch die Umwandlung kerninnerer Protonen in - nur dort dauerstabile -
Neutronen) stets kleiner ist, als das aus der Ursprungsrechnung hervorgeht
Länger als 17 Kettenglieder lang kann die (geschlossene) Kernringkette jedoch sehr wohl sein. Dann ist sie aber nicht mehr ganz fest gewickelt und
gespannt und enthält demnach außen keine zu Neutronen umgewandelten Protonen mehr. Es ist dies abseits etwaiger Kernmagie die ganz banale Erklärung für die dort gefundene “magische” Neutronenzahl 82. -
Noch etwas banaler und trivialer ist nach einer auffälligen Lücke bei der Kernmassenzahl nur das Zustandekommen der leichteren Spaltfragmente,
die ja quasi automatisch aus dem verbleibenden Rest, abzüglich sonstiger (Strahlungs-)Verluste resultieren. U. a. findet man hier radioaktive
Strontium-, Zirkonium, Molybdän- und Technetium-Isotope. Die spannende Frage ist nur: Wie sind diese Kerne nun eigentlich wieder hinlänglich stabil
aufgebaut, nachdem ja auch die Neutronenzahl 50 ebenfalls auf magische Weise sieben stabile Isotope von Kr-86 bis Mo-92 zu verbinden scheint?!
Ein Knoten in der Kette ist, wie zuvor ausgeführt wurde, an dieser Stelle noch nicht möglich, was aber dann - irgendetwas muß es doch sein! Die
richtige Lösung kann man - mangels Computermodell - jetzt immer noch am besten mittels Perlenmodell finden. Beim “Spielen” mit dem nach der
Abspaltung von Cäsium-136+ verbliebenen Rest von 12 Kettengliedern kommt man so zur einzig möglichen stabilen Lösung für Mo-96 und die
darauf aufbauenden Folgekerne: Die Kette ist nunmehr um 360° + 90° in sich verdreht und verspannt. Das ist ähnlich wie bei einem Gummimotor -
mit dem entscheidenden Unterschied, daß sich auf diese Weise hier die Energie des Kerns nicht vergrößert, sondern verkleinert. Es können sich so
im geschützten Kerninnern wiederum Protonen - energiemindernd - in nunmehr stabile Neutronen umwandeln.
Wenn man das einmal verstanden und akzeptiert hat, ist es nur noch ein kleiner Schritt, eben diese überzeugende Lösung (mit der Formel 7x 8
Nukleonen) auch auf Fe-56 anzuwenden. Bekanntlich findet man bei den mittelschweren Nukliden im Bereich von A = 56...62 die Kerne mit den
absolut größten Bindungsenergien pro Nukleon. - Allerdings wird man bereits beim Erstellen des nebenstehend gezeigten sehr kompakten Modells feststellen: Die bei dieser Kernstruktur nunmehr auftretende
Torsionsspannung ist wesentlich größer als beim vorigen Beispiel. Zum anderen sollten hier folglich nicht nur zwei Protonen in Neutronen
umgewandelt worden sein, sondern eher vier oder sogar sechs, d. h. es müßte sich deshalb um die instabilen Isotope Cr-56 oder Ti-56 handeln.
Beim entsprechend weniger verspannten, dafür aber eher unförmigen (mit über 91% häufigsten) Eisenisotop Fe-56 drängt sich im Gegenzug nun
jedoch eine neue Vermutung auf: Die nach allgemein gängiger Auffassung strukturbedingten ferromagnetischen Eigenschaften von Eisen, Kobalt und Nickel sollten nach dem Kernmechanischen Modell letztlich wiederum auf
die hier stark asymmetrischen Kernstrukturen zurückgehen!
Wenn dem wirklich so wäre, sollten sich hier meßbare Unterschiede bei
der Suszeptibilität zum vorhergehenden leichteren und (mit 5,8% Anteil) selteneren Eisenisotop Fe-54 zeigen. Wahrscheinlich wäre Fe-54 dann ebenfalls nicht mehr ferro- sondern nur noch paramagnetisch?!
Die Feststellung, die Bindungsstrukturen der chemischen Elemente hingen nur von der Ordnungszahl der Atom(kern)e ab, klingt plausibel und stimmt
im allgemeinen wohl auch; - meistens - aber eben nicht immer. Derartige von Menschen gemachte Gesetze, ganz gleich wie weitgehend sie auch
akzeptiert sein mögen (wie etwa die Heisenbersche Unschärferelation), können fehlerhaft sein. Sie müssen deshalb immer wieder, oder überhaupt
erst einmal, auf den Prüfstand gestellt werden - manches wurde nur behauptet und niemals überprüft. Vom Grundsatz her sind sie jedoch tatsächlich eben keine “Naturgesetze”.
Jeder Wissenschaftler sollte sich dessen bewußt sein und sich vielleicht mal hin und wieder die wissenschaftskritischen Überlegungen von Karl
Popper oder Paul Feyerabend zu Gemüte führen - auch wenn diese heute nicht mehr so sehr “in” zu sein scheinen.
Widersprüche zur geltenden Lehrmeinung zeigen sich in der Physik und Kosmologie derzeit überall und wenn es nur um neue Multiquarks geht, welche nun aus (nicht vier oder fünf, sondern aus) sechs Quarks bestehen, so ist dies für die Kernmechanik nichts Neues und entspricht den doppelt besetzten Nukleonen-Orbitalen. Da es hier aber auch Dreifach-Orbitale
gibt, fällt die Prognose für das Auffinden weiterer Neunfach-Multiquarks nicht schwer...
|