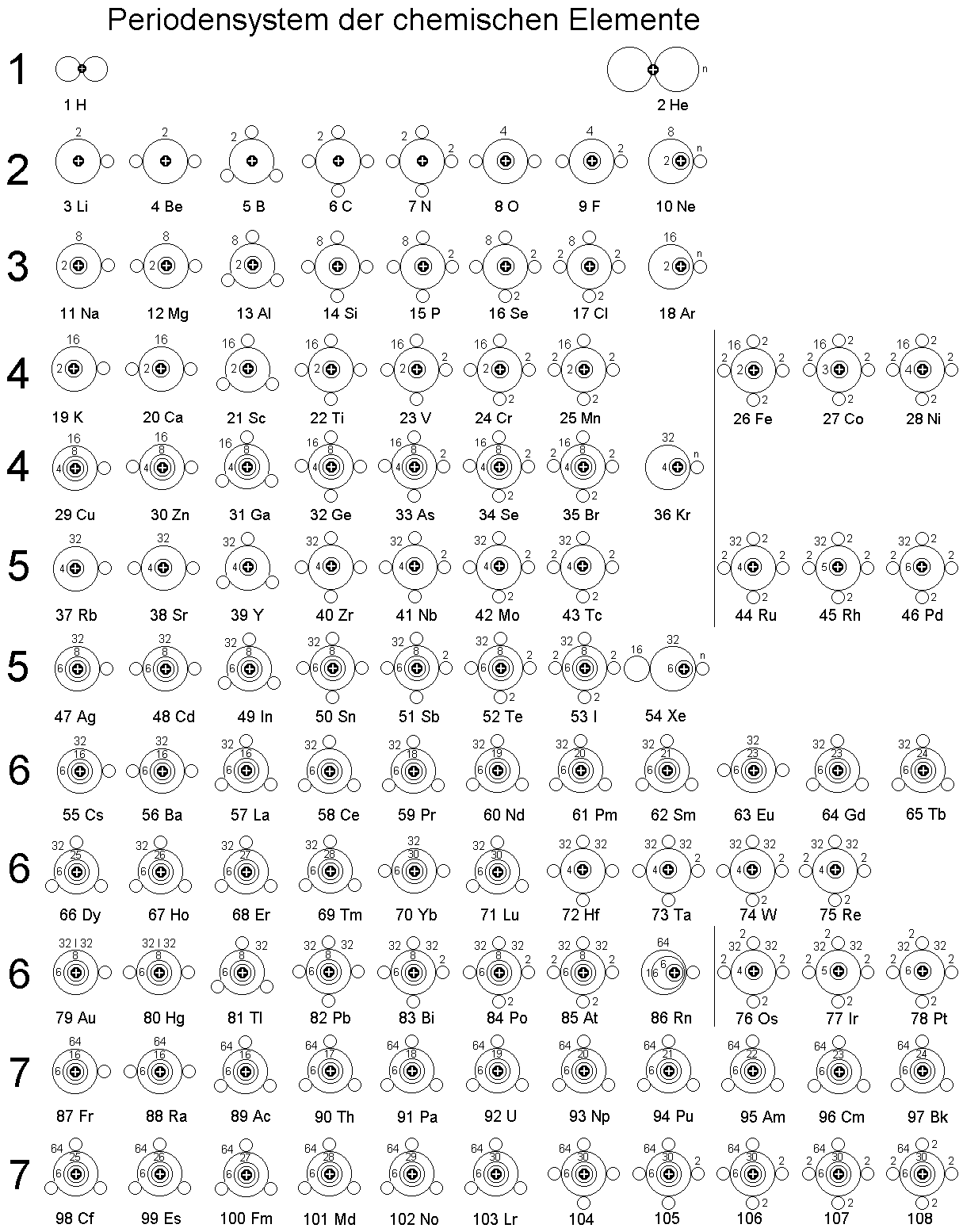|
Kernmechanische Elektronenringe und Atomspektren
Wenn im Rahmen der Kernmechanischen Chemie zuletzt die Rede war von Elektronenringen mit mehr als zwei Elektronen und jeweils besonderen Eigenschaften (aromatischer 6-Elektronenring, Oktett-Ringstruktur), muß man sich irgendwann natürlich auch die Frage stellen, wie real ist das alles? In der Physikalischen Chemie spricht man ja zum Beispiel nur von Aufenthaltswahrscheinlichkeiten oder “delokalisierten” Elektronen usw..
Der schwierigste aber wohl auch überzeugendste Weg bestünde darin, einen Zusammenhang mit den charakteristischen Atomspektren der chemischen
Elemente aufzuzeigen oder gar die dahinter verborgene Mechanik. Genau dies soll hier nun versucht werden, - wobei das größte Hindernis in der quasi selbstverständlich angewendeten, etablierten Quantenmechanik liegt.
Ein wichtiger Hinweis kommt dabei aus der genauen Kenntnis der gut erforschten sogenannten Rydberg-Atome. Das sind durch Stoßprozesse oder
Lasereinstrahlung hoch angeregte wasserstoffähnliche Atome, wo sich ein Elektron etwa mit einer Hauptquantenzahl von n = 60 weit entfernt vom Atomrumpf befindet. Dabei kann der Radius, der mit dem
Quadrat von “n” anwächst, ohne weiteres makroskopische Dimensionen erreichen und z.B. zweitausend Angström betragen. Auf Grund der sehr schwachen Bindung reagieren Rydberg-Atome deshalb auch extrem
empfindlich auf elektrische Felder. -
In Kenntnis all dieser Gegebenheiten liegt es nun ziemlich nahe, hier einen Kernmechanischen Zusammenhang herzustellen und die Kernringe mit den spektroskopisch ermittelten Energieniveaus zu verbinden, was ja a priori schon mal logischer erscheint, als Niels Bohrs erlaubte und verbotene Elektronenbahnen oder die sodann rein mathematisch begründeten durch die jeweiligen Quantenzahlen festgelegten Elektronen-Orbitale, die letztlich ebenfalls zum gewünschten Ergebnis führen.
Setzt man dagegen für die dimensionslose Hauptquantenzahl “n” nunmehr n Elektronen in die Rechnung ein, ergeben sich die
beobachteten Spektrallinien ganz zwanglos fast von selbst. Trotzdem geht die Rechnung scheinbar nicht ohne weiteres gleich auf: Die Atomspektren werden ja jeweils dem neutralen Atom (hier: Lithium)
zugeschrieben, während die so genannten Funkenspektren auf Grund des scheinbaren Elektronenmangels und der positiv geladenen Ionen in ihrer Struktur um eine Kernladung, also um Z = -1, (“nach links”)
verschoben erscheinen. Die Alkalispektren gleichen dann denen der vorangehenden Edelgase und beim ionisierten Wasserstoff - ohne “Leuchtelektron” - gibt es überhaupt kein Spektrum. -
So weit, so logisch aber vermutlich dennoch falsch: Vielmehr sind die Funkenspektren nämlich die neutralen, während die Entladungsspektren auf
Grund der stattfindenden Ionisierung mit hohen Elektronenüberschüssen in Verbindung gebracht werden müssen. Dann enthielte etwa der leuchtende Wasserstoff folglich einen Elektronenring mit mindestens
zwei, in höher angeregten Zustanden aber noch weitaus mehr Elektronen; siehe auch die (wasserstoffähnlichen): Rydberg-Atome! Das gilt analog ganz ähnlich ebenso für die Alkalimetalle.
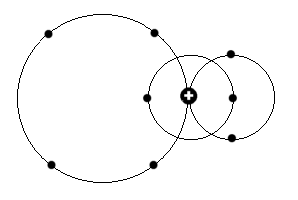 1. Alkaliatom-Orbitalschema 1. Alkaliatom-Orbitalschema
Wenn man in obiger Schemazeichnung die beiden mittleren Elektronen entfernt, entspricht diese einem Wasserstoffatom mit n = 2, bzw. 4.
Dagegen ergibt sich durch das Entfernen eines der beiden äußeren Ringe das Singulettschema von Helium, wobei nur bei parallelem Drehimpuls n
auch gleich 1 sein kann. Ansonsten ändert sich in einem bestimmten Atom der jeweilige Drehimpuls sprunghaft dann, wenn ein Kernring oder
Elektronen daraus entfernt werden. Genau das korrespondiert mit der Emission von Lichtquanten, also Photonen.
Was geschieht nun aber mit den abgesprengten Elektronen(ringen), die ja über ihren Drehimpuls auch Energie mit sich führen und durch Reflektion
wieder auf das energieärmere Atom zurückübertragen können; wenn sie die Energie dagegen weiter (mit Lichtgeschwindigkeit?) forttragen würden,
- hätten sie dann nicht all die Eigenschaften, wie man sie eben gerade den Photonen zuschreibt?!
Übrigens gibt es aber noch einen weiteren aktuellen starken Hinweis, wenn nicht gar Beweis, für die Existenz der grundlegenden Elektronenringe. Im
Georgia Institute of Technology wurden kürzlich Versuche mit ganz präzise in Ätztechnik erzeugten schmalen Graphen-Streifen durchgeführt, wobei sich hier eine ganz signifikant erhöhte Leitfähigkeit und -geschwindigkeit zeigte, was anderweitig kaum erklärbar erscheint.
Von den vier Valenzelektronen eines Kohlenstoffatoms werden bei Graphit
oder Graphen drei Elektronen für eine gesättigte (2-Elektronen-)Bindung zu den jeweiligen drei Nachbaratomen benötigt, wobei diese Bindungsringe
senkrecht zur Graphen-Ebene orientiert sind. Bleibt also pro C-Atom noch ein freies Elektron in der Wabenebene für den Ladungstransport übrig. Rein
rechnerisch entfallen auf einen nur zwei Wabenreihen breiten Leitungsstrang dann im Durchschnitt drei Elektronen auf jede Wabe, während es bei unendlich breiten Graphen-Bändern dann - im Schnitt - nur
zwei sind.
An sich würde dies schon für eine fast perfekte Leitfähigkeit reichen, wenn denn die jeweils pro Wabe vorhandenen zwei Elektronen nun immer
diamagnetische 2-Elektronenringe ausbilden würden. Da aber hier - im Gegensatz zu einem Benzolring mit sechs Elektronen - in der Ebene
genügend Platz vorhanden ist, ist das Resultat aber ein nicht optimales Zufallsgemisch aus Ein- und Zwei-Elektronenringen.
Genau dies ist auch die Erklärung für die wesentlich bessere Leitfähigkeit der schmalen Graphen-Bänder. Trotzdem ist dies aber noch kein
hinreichendes Kriterium für die Supraleitung. Diese kann erst dann
stattfinden, wenn durch eine geeignete Schichtenanordnung eine mit wenig Atomen besetzte und somit kollisionsfreie Supraleitungsebene für die (auch Cooper-Paare genannten) 2-Elektronenringe vorhanden ist.
Das Wasser (-molekül) der Erkenntnis
Wasser kann mit entsprechendem Energieeinsatz leicht in seine Bestandteile Wasserstoff und Sauerstoff gespalten werden und auf diese
Weise ein Maximum an chemischer Energie speichern,- die etwa bei der heftigen Verbrennung des per Elektrolyse gebildetem Knallgases wieder
freigesetzt wird. Das Geheimnis der großen Energieeffizienz ist dann aber wohl vor allem in der besonderen Elektronenanordnung des Sauerstoffs zu
suchen, als in der einfachstmöglichen Struktur des nur aus einem Proton und einem Elektron bestehenden Wasserstoffatoms.
Nach dem überkommenen (und wahrscheinlich überholten) Schalenmodell soll ja die innere “K”-Elektronenschale des Sauerstoffatoms mit zwei
Elektronen in der Edelgaskonfiguration des Heliums besetzt sein und die zweite, die “L”-Schale mit den beiden zusätzlichen Wasserstoffelektronen -
also hier insgesamt acht Elektronen - ebenfalls die Edelgaskonfiguration des Neons erreicht haben.
Das kann aber noch nicht die ganze, bzw. richtige Erklärung für die heraus ragenden Eigenschaften des Wassermoleküls sein und Kernmechanisch
gilt das natürlich erst recht!- Da es aber im Kernmechanischen Modell des Sauerstoffs jeweils zwei (antiparallel) ausgerichtete Protonenorbitale gibt,
welche rechtwinklig zueinander stehen und auch die Elektronen-Orbitale bestimmen, ist es dann nur logisch, wenn es nun ebenfalls zwei rechtwinklig
angeordnete Elektronenringe gibt, - dank dem Wasserstoff - aufgestockt auf je vier Elektronen. -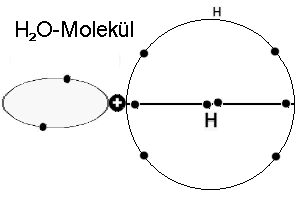
Elektronen-Orbitale des Wassermoleküls mit zwei senkrecht aufeinander stehenden und mit einander synchronisierten Vier-Elektronenringen. Der
ursprünglich innere, mit zwei Elektronen besetzte “K”-Ring erscheint nach außen gedrängt und ist, gemeinsam mit den beiden Wasserstoffatomen mit
dem charakteristischen Bindungswinkel verantwortlich für das sehr große elektrische Dipolmoment des Moleküls.
Zum Vergleich: Beim Schwefelwasserstoff - mit nunmehr zwei senkrecht aufeinander stehenden Acht-Elektronenringen - sind die beiden (auch für
den Geruch “nach faulen Eiern” verantwortlichen) externen H-Protonen derart schwach gebunden, daß beim Zerfall des Moleküls Energie frei wird.
Ganz im Gegensatz zur exothermen Knallgasreaktion bei der Bildung von Wasser; - dessen absolute Geruchs- und Geschmacksneutralität auf der
starken Bindung der externen H-Protonen an die beiden 4e-Ringe beruht.
Orbitalmodell - ohne innere “K”.Schale, die in den ersten drei Perioden
genau zwei Elektronen enthält und dann in der vierten und fünften Periode um jeweils zwei weitere Elektronen - auf maximal sechs - aufgestockt wird.
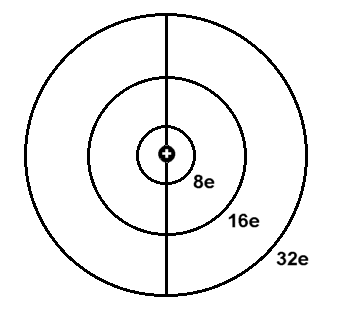
Da die Elektronenringe (“Schalen”) nacheinander jeweils doppelt ausgebildet werden können, reicht dieses sehr einfach strukturierte
Orbitalmodell genau bis zum Element 118, das nach dem Komplettieren der zweiten äußeren 32-Elektronenschale eigentlich ein Edelgas wäre, aber eben auch keinen Platz mehr für “Leuchtelektronen” bietet?!
Von oben gesehen sehen die abgeschlossenen Elektronenschalen im Prinzip so aus: Grafik links. Wenn zur Edelgaskonfiguration von Xenon noch
weitere Elektronen hinzu kommen, werden diese bei Cäsium und Barium zunächst sehr lose, außen gebunden, wie das bei den leichteren Alkali- und Erdalkalimetallen ebenso der Fall ist.
Danach scheint aber bei den darauf folgenden 14 Seltenerdmetallen eine
andere Konfiguration - rechte Grafik - offenbar energetisch günstiger, wobei sich die gesamten äußeren Elektronen (maximal 16) zu einem einzigen
exzentrischen Elektronenring gruppieren. Genau dieser Umstand ist aber mit der besonders großen Suszeptibilität der stark paramagnetischen Lanthan(o)iden verbunden.
Es muß hier aber betont werden: Dies ist zunächst nur ein theoretisches Erklärungsmodell, das analog zum Schalenmodell der Physikalischen
Chemie davon ausgeht, daß die jeweiligen “Schalen” oder Elektronenringe chronologisch nacheinander mit Elektronen besetzt werden und diesen Zustand dann auch beibehalten. Wie das neue Kernmechanische Periodensystem am Ende der Seite zeigt, ist dies aber durchaus nicht so: Elektronenringe werden aufgebaut und abgebaut oder durch größere
ersetzt, wie es zum Erreichen der Zustände mit der jeweils geringsten Energie gerade notwendig ist.
 1. Alkali-Atommodell* 1. Alkali-Atommodell*
Das weiter oben bereits kurz angesprochene Alkali-Atommodell - es ist
immer mit einer Dublettstruktur verbunden - soll nun noch etwas genauer untersucht werden, zumal es auch beim Kernmechanischen Atommodell
zwischenzeitlich mehrfach zu einem Wechsel der Auffassungen, bzw. zu unterschiedlichen Interpretationen der grundlegenden Elektronenstrukturen
bei der Emission von Photonen gekommen ist.
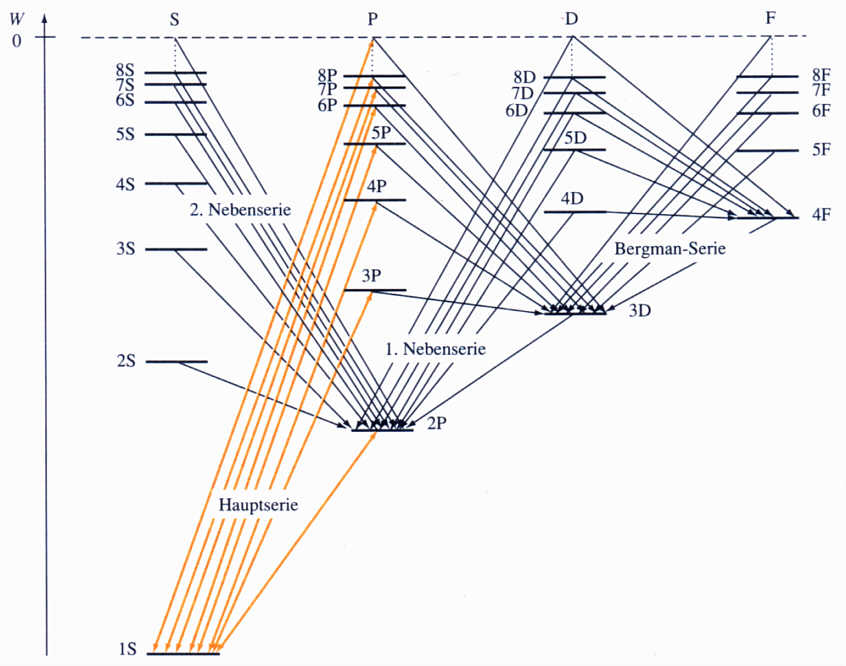
Das passende Energieschema für alle Alkaliatome, immer beginnend mit den gleichen Haupt- und Nebenquantenzahlen, das aktuell erst erstellt
werden sollte, gibt es erstaunlicherweise bereits: Abb. 7.1, S. 208, Hänsel / Neumann “Physik”, Atome.Atomkerne.Elementarteilchen, Spektrum Akademischer Verlag 1995, ist dort aber nur schematisch zu verstehen, in
der KM Chemie jedoch real, quasi “wörtlich” zu nehmen!
Noch ein wichtiger Punkt ist die “quantenmechanische Teleportation”, die scheinbar durch das Bellsche Theorem bewiesen - und damit Einsteins EPR-Annahme zugleich widerlegt wurde, zumal die Bellsche Ungleichung verborgene Variable - Stichwort: lokal contra nicht lokal - grundsätzlich
ausschließen konnte. Erst durch die Messung wird demnach der Zustand zweier korrelierter Photonen, der bis dahin noch unbestimmt ist, festgelegt.
Übersehen wird dabei aber, daß die Ungleichung auf fragwürdigen Hilfsannahmen beruht, welche die dreidimensionale Ausrichtung der miteinander korrelierten Photonen in ihrer Polarisation unzulässigerweise
auf eine Ebene reduziert. Da die Photonen offenbar jedoch zugleich linear und zirkular polarisiert sein können, widerspricht das Ergebnis nun gerade
eben nicht mehr den von Einstein propagierten verborgenen Variablen!
Von besonderem Interesse in der gesamten Teilchenphysik ist schließlich noch der Mechanismus, der bei allen (geladenen) Elementarteilchen Masse
generiert, was ja durch die in Teilchenbeschleunigern aufgespürten relativ schweren und kurzlebigen “Higgs-Teilchen” nach Ansicht von vielen
kritischen Physikern nicht wirklich erklärt wird. Beim Kernmechanischen Modell wird dagegen bei geladenen Elementarteilchen angenommen, daß
diese gleichzeitig um mindestens drei zueinander senkrechte Drehachsen rotieren, was diesen somit mechanisch unmittelbar Masse verleiht!
Bleibt u. a. noch eine Frage: Wenn die emittierten Photonen mit genügend kurzer “Wellenlänge” und entsprechend großer Energie in der Lage sind,
Elektronen aus Alkalimetallen heraus zu schlagen und die Leitfähigkeit von Halbleitern zu erhöhen, bzw. eine direkt dort ableitbare Spannung zu liefern,
könnten sich die so erzeugten Photonen nicht wieder in Elektronen zurück verwandeln; - und bei der Erzeugung über Antimaterie in Positronen?
Dem stehen nun allerdings gleich zwei entscheidende Tatsachen entgegen: 1. Wenn dies wirklich so wäre, müßte die Emission von Photonen mit einer
positiven Ladungsänderung verbunden sein. Das ist offenbar nicht der Fall!
2. tritt bei der Analyse von Photonen aus Antimaterie keine Annihilation
(Vernichtungsstahlung) durch etwaige Positronen auf. Plausibel ist jedoch, daß die Absorption von Photonen bei Alkalimetallen, quasi spiegelbildlich, genauso “ladungsneutral” verläuft wie deren Emission! - Was nach alledem
immer wahrscheinlicher wird, ist die Erkenntnis, daß die scheinbaren Welleneigenschaften der Photonen und Elementarteilchen bei der Beugung am Doppelspalt allein durch den äußeren Spin der Partikel erklärt werden
kann.
Wenn sich also, wie oben aufgeführt, Elektronen, Photonen und sonstige Elementarteilchen auf Grund ihrer elementaren Spineigenschaften ständig
auf Kreisbahnen um den eigenen (leeren) Schwerpunkt bewegen, dann können sie sehr wohl auch durch beide Doppelspaltöffnungen gehen; - nicht gleichzeitig, sondern nacheinander und auch mehrmals!
Bei den Elektronen wurden diese Ringbahnstrukturen, ohne die es ja eine singuläre Massenkonzentration in einem Punkt gäbe, ausführlich begründet
und beschrieben. Bei den Eigenschaften elektromagnetischer Wellen wurde weiterhin ebenfalls gefunden, daß diese einen Tunnel, der kleiner ist
als die jeweilige Wellenlänge, allenfalls stark abgeschwächt passieren...
Man kann den Durchgang von Elektronen, Photonen usw. durch einen Doppelspalt oder ein Beugungsgitter auch sequentiell betrachten, d. h. das
Teilchen (Quant) muß das genannte Hindernis zunächst einmal passieren und trifft dann auf dessen Rückseite wiederum in seiner Kreisbewegung auf
die Spaltöffnungen, was somit bestimmte Fortbewegunsrichtungen wahrscheinlicher und andere wiederum unwahrscheinlicher macht. Es
leuchtet unmittelbar ein, daß ein periodisches Beugungsgitter diesen Effekt potenziert und verstärkt, so daß die Minima und Maxima hier noch deutlicher hervortreten.
Elektronenkonfiguration beim Wasserstoffspektrum u. a.
Weiter oben wurde das Spektrum des Wasserstoffatoms ja bereits einer ersten Analyse unterzogen, wobei bereits festgestellt wurde, daß ein
neutrales (Funken-) Spektrum hier überhaupt nicht existiert und daß es darüber hinaus schwierig ist, sich aus den überlieferten Denkstrukturen der
etablierten Quantenmechanik zu lösen. - Erste Folgerung: Nur durch den Elektronenbeschuß oder eine genügend starke Erwärmung des Gases
entstehen auch negativ geladene Wasserstoffionen, welche nun leuchten und somit - im Vergleich zu allen anderen - das am einfachsten strukturierte Spektrum überhaupt bewirken bzw. hervorrufen.
Zur Illustration der Wasserstoff- und Alkalispektren soll das im Vergleich
zum Wasserstoff nur unwesentlich kompliziertere Lithium-Spektrum, Abb. rechts, herangezogen werden. Dies auch deshalb, weil dort die Entartung
zu gleichen Energieniveaus aufgehoben ist. So fallen beim Lithium und den anderen Alkaliatom-Spektren etwa die Zustände 1s und 2p, 3s, 3p und 3d
nicht mehr energetisch auf einer Stufe zusammen, sondern erscheinen hier - auch räumlich - deutlich getrennt voneinander. Dabei lassen sich auch die Unterschiede zwischen der bisherigen Quantenmechanik und der neuen Kernmechanik besser herausarbeiten.
Bisher stehen die Bezeichnungen s, p, d, f usw. für die verschiedenen jBahndrehimpuls-Quantenzahlen, wobei nun definitionsgemäß bedeutet der
Bahndrehimpuls L ist bei “s” nun gleich Null. Ebenso steht der Buchstabe “p” für einen Bahndrehimpuls 1; - “d” steht für L=2 und “f” für L=3 usw..
In der Kernmechanik ist das etwas anders: Schon bei den Atomkernen steht etwa ein nuklearer Bahndrehimpuls I = 1/2 oder auch I =1 für den
resultierenden Drehimpuls - Kernspin - der in Kernringen angeordneten Nukleonen, der allerdings bei perfekter Spinpaarung (He-4 od. O-16 und
anderen gg-Kernen) ebenso Null sein kann. Dennoch kommt er dort, wie auch in der Atomphysik, nicht durch den quantenmechanisch postulierten
Bahndrehimpuls zustande, sondern durch die (ggf. vektorielle) Addition der jeweiligen Teilchenspins von Nukleonen oder Elektronen (Leptonen).
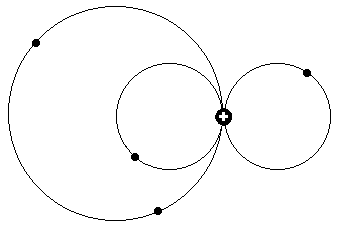
Ein “Bahndrehimpuls p” (L= 1) heißt also in der untenstehenden Zeichnung:
auf der linken Seite befindet sich nun etwa gerade ein Elektron, während es bei “d” (L=2) demnach zwei Elektronen sind. Die Zahl der Elektronen auf
der rechten Seite - Anordnung willkürlich gewählt - steht danach für die für die verschiedenen mit der Hauptquantenzahl n steigenden Energieniveaus
der in den Spektren nebeneinander angeordneten Leitern s, p, d, f usw..
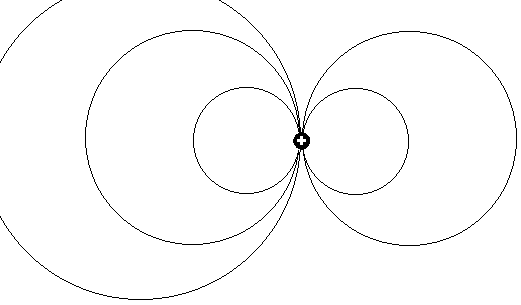
In der nächsten Zeichnung, unten, ähnelt die Elektronenkonfiguration auf der
rechten Seite bezüglich der Feinstruktur wiederum dem obigen Beispiel, nur daß dem rechten Zwei-Elektronenring hier auf der linken Seite nunmehr Ringe mit einem, zwei oder auch drei Elektronen gegenüber stehen, was ja,
in einem früheren Erklärungsmodell mit als Photonen abspringenden Elektronen zu gleichen Energieniveaus im Termschema führen sollte.
Offenbar ist dieses nicht wirklich konsistente alte Modell aber nun überholt.
Wenn es um ein wirklich logisches Modell für den Mechanismus bei der Photonenemission geht, haben beide Erklärungsmodelle systemimmanent
Schwächen an unterschiedlicher Stelle: Die Quantenphysik benötigt hilfsweise den Einsatz rein theoretisch mathematisch definierter “Quanten”,
um die die Erzeugung von Photonen durch Elektronen - beides eigentlich sehr ähnliche “Schwesterteilchen” (gleiche Beugungsbilder und mehr) - zu begründen. und auch das Kernmechanische Erklärungsmodell war in der
bisherigen Form nicht durchweg konsistent oder logisch! - Das einfache durch elektrostatische Energie bewirkte Absprengen von Elektronen erklärt
ja noch nicht wirklich deren Umwandlung in Photonen oder warum diese Energie gerade beim besonders stark gebundenen Singulett-Grundzustand von Helium auffälligerweise mit Abstand am größten ist.
Alles ist anders - ein neuer Ansatz
Tatsächlich ist alles aber wohl ganz anders und deutlich einfacher, als es
zuletzt beschrieben wurde. Schließlich kommt die Photonenemission in den Atomspektren ja offenbar nicht dadurch zustande, daß Elektronen etwa von
einer höheren Bahn in einem “Quantensprung” auf eine niedrigere Bahn springen, auch nicht, weil diese die in Ringen gespeicherte elektrostatische
Energie beim Absprengen nun als Photonen wieder abgeben, sondern, weil der Mechanismus genau der gleiche ist, der auch beim Positronium, jener
sehr kurzlebigen quasimolekularen Verbindung aus Elektron(en) und Positron(en) die Umwandlung von Leptonen in Photonen bewirkt.
Im Vergleich mit einem normalen Wasserstoffatom sind beim Positronium
sowohl Radius als auch die Wellenlängen der emittierten Strahlung doppelt so groß, bevor im Grundzustand Vernichtungsstrahlung - etwa in zwei
Gammaquanten von 0,511 MeV (aus dem Singulett-Zustand) - auftritt.
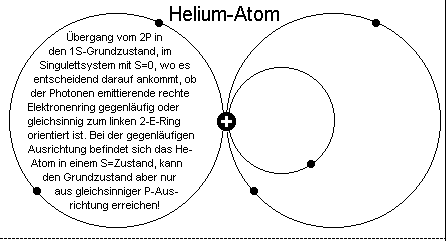
Genau das ist nun auch das - jetzt weitgehend mit der Quantenphysik kompatible - modifizierte Kernmechanische Erklärungsmodell
der Strahlungserzeugung, wobei sich eben auch hier die sich zunächst auf antiparallelen Bahnen aufhaltenden metastabilen Elektronen durch eine
geringe Energiezufuhr von 2S in 2P- Elektronen (-ringe) umwandeln. Danach stoßen die auf parallelen Bahnen und somit auf Kollisionskurs befindlichen Elektronen im He-Grundzustand
zusammen, wobei sich nun - wie beim Positronium - die Elektronenmasse (der Elektronen auf der rechten Seite) komplett in Strahlungsenergie, also Photonen oder auch Quanten, umwandelt.
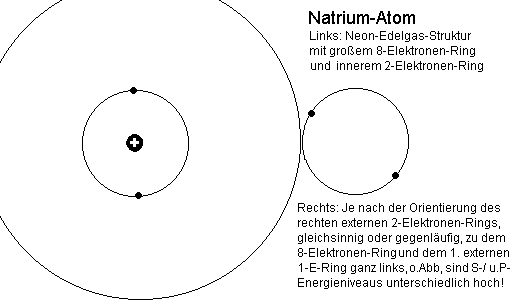
Besonders gut sichtbar und erklärbar sind die Vorgänge beim Natrium, wenn man zunächst einmal von der auffälligen und charakteristischen
Dublettstruktur des Spektrums ausgeht, welche bereits beim Übergang zwischen dem Grundzustand und dem ersten angeregten Zustand (gelbe Doppellinie) zu beobachten ist.
Beim Natrium-Spektrum, welches ja anders als die Edelgase Helium und zuletzt Neon, nun auf einer abgeschlossenen inneren Schale (eigentlich
einem - inaktiven -Ring) aufsetzt, kommen die unterschiedlichen Energie- Niveaus allein dadurch zustande, wie der aus einem oder mehr Elektronen
bestehende Leuchtelektronenring zum anderen orientiert ist. Bei den so genannten 3P-Niveaus ist, abgesehen von der Elektronenzahl, allein
entscheidend, daß sie sich in der gleichen Ebene wie der Edelgasring befinden und ob die Orientierung der Drehringe gleichsinnig oder
gegenläufig zueinander ist. Es ist jetzt auch unmittelbar einsichtig, daß die gegenseitige Ankopplung der beiden Ringe durch starke Magnetfelder beeinflußt wird, siehe: anomale Dublett-Aufspaltung.
Etwas, das die bisherige eigentlich bereits überholte Quantenphysik nicht
wirklich erklären kann - dort gibt es nur empirische Auswahlregeln, etwa für erlaubte (beobachtete) Übergänge zwischen den benachbarten Leitern des
Grotrian-Spektrums, die aber nur sagen, was ist und nicht warum das so ist, wird erst bei einer detaillierteren Betrachtung offenbar. Scheinbar ist ja beim Natrium-Spektrum
alles in Ordnung: Übergänge gibt es nun nur zwischen benachbarten Leitern; - aber warum gibt es solche Übergänge zwischen den 4P-Niveaus zum 4S-Niveau und dann (schon) wieder zurück
zu den 3P-Niveaus? Derartiges ist ja beim Helium nicht zu beobachten!
Kernmechanisch gibt es aber einen wichtigen Unterschied zwischen He und
Na: Damit das Heliumatom nicht einfach ein energiereicheres H-Spekrum abstrahlt, gibt es nun einen zweiten (“angeregten”) Elektronenring zu dem
Zweck. Der aber ist, anders als beim Natrium, im Grundzustand nicht mehr vorhanden. Natrium benötigt den Ein- oder Mehrelektronenring auch im
Grundzustand und ist demnach bei der Strahlungsemission bis zuletzt damit verbunden, während er bei Helium am Ende komplett entfernt wird. Im
Natrium-Termschema, rechts, sind die L-Elektronen (gemäß dem vorigen Abstoßungsmodell!) extra eingezeichnet. Wie bereits weiter oben erklärt
wurde, lassen sich insbesondere bei den Alkalimetallen aus der Besetzung der Elektronenringe mit Elektronen alle Parameter unmittelbar ableiten.
Besonders deutlich wird die Anordnung der jeweiligen Energieniveaus, wenn man einmal die Spektren von Lithium und Natrium vergleicht:
Ein “Bahndrehimpuls p” (L= 1) heißt also in der untenstehenden Zeichnung: auf der linken Seite befindet sich nun etwa gerade ein Elektron, während es
bei “d” (L=2) demnach zwei Elektronen sind. Die Zahl der Elektronen auf der rechten Seite - Anordnung willkürlich gewählt - steht danach für die für
die verschiedenen mit der Hauptquantenzahl n steigenden Energieniveaus der in den Spektren nebeneinander angeordneten Leitern s, p, d, f usw..


Bei beiden Alkalimetallen gibt es einen mittleren Edelgas-Elektronenring.
Beim Lithium mit der Kernladung +3 ist dies ein Heliumring mit zwei Elektronen, beim Natrium mit der Kernladung +11 aber zusätzlich nun ein
Elektronenring mit acht Elektronen. Der zweite links befindliche Ring ist hier nicht gezeichnet. Wenn er aber tatsächlich ganz fehlt, gibt es keine P-Leiter und demzufolge auch kein Alkalispektrum.
Gemäß der obigen Erläuterungen stehen die jeweils linken Elektronenringe
für den “Bahndrehimpuls” L= 0 bis 3 (s, p, d, f...), während die Ringe auf der rechten Seite die Hauptquantenzahl bezeichnen. - Hierbei gibt es nun
signifikante Unterschiede zwischen den Alkaliatom-Spektren in Bezug auf die jeweils untersten d-Niveaus des Li-und des Na-Spektralsystems, welche
sich direkt hieraus erklären lassen. Beim Lithium sind die Energieniveaus von 3p, 3d und dem von Wasserstoff fast gleich, während das beim Natrium erklärlicherweise ganz anders ist.
Der Aufbau des Periodensystems der chemischen Elemente erforderte ebenfalls eine genauere Untersuchung, zumal mit der summarischen Aufzählung der Elektronenringe oder Schalen noch nicht alles gesagt ist,
andererseits u. a. auch bestimmte Eigenschaften, wie die magnetische Suszeptibilität direkt aus den Ringstrukturen abgeleitet werden können.
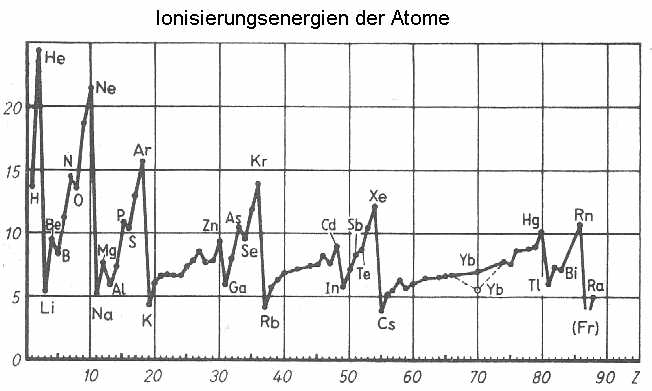
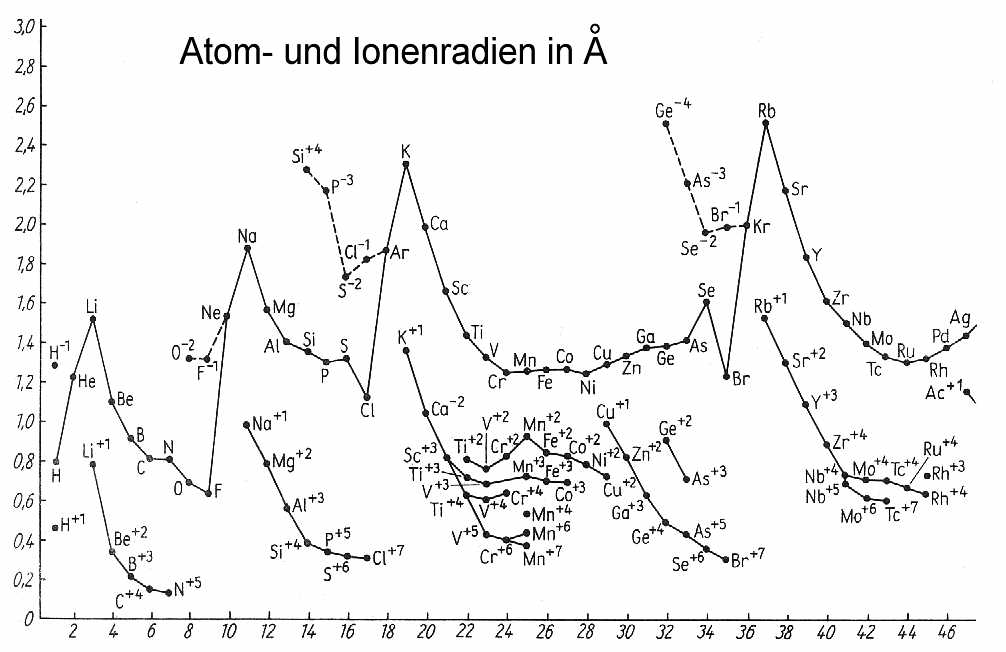
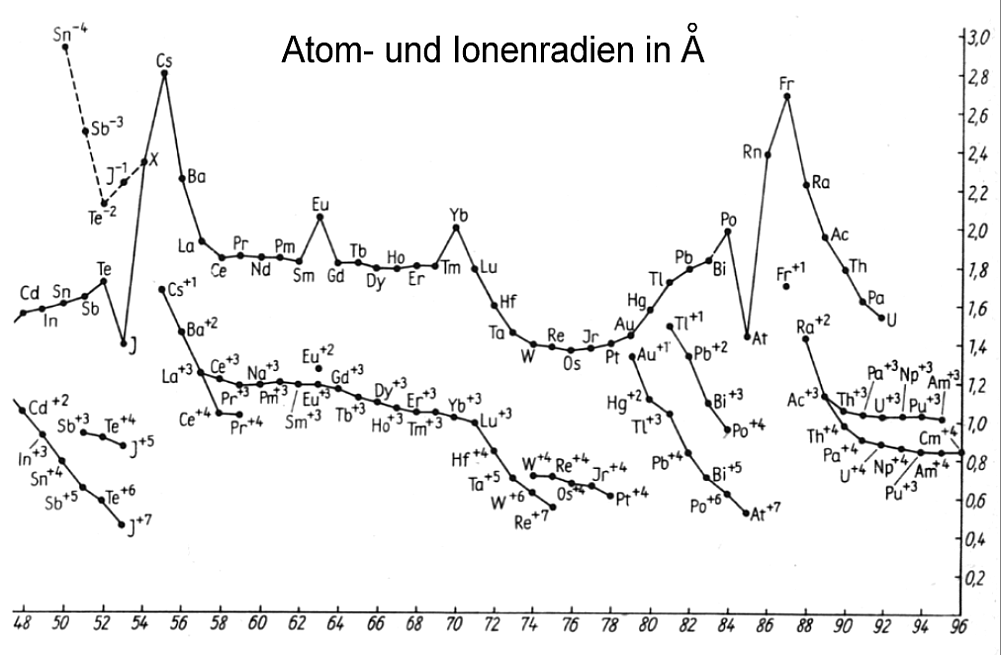
In der ganz konkreten Anordnung aller Ringelektronen erkennt man nun sofort, warum etwa der Atom- und Ionenradius beim Übergang von der
Hauptgruppe VII zur Edelgasgruppe VIII sprunghaft zunimmt, was beim rein formalen und unlogischen quantenmechanischen Periodensystem nicht der
Fall ist. Man sieht außerdem ebenfalls, was in der (Eisen-)Nebengruppe VIIa tatsächlich passiert, oder wann genau in einem Elektronenring die
maximale Besetzungszahl erreicht ist und folglich ein Strukturwechsel stattfindet. - das passiert schon bei 30 und nicht erst bei 32 Ringelektronen
- oder wann bei den Lanthanoiden und Actinoiden erst einmal innere Elektronen-”Schalen” aufgefüllt werden, bevor es wieder normal weitergeht.
Überhaupt geht es auch gar nicht streng systematisch oder chronologisch zu: Einmal besetzte Elektronenringe können bei Bedarf wieder aufgelöst
oder reduziert werden, wenn dies für die energetische Gesamtbilanz des Atoms günstiger ist.
Ähnliches gilt sinngemäß auch für gewählte grafische Darstellung dieses Periodensystems, wo vorrangig jedoch auf eine ökonomische Platznutzung
und gute Erkennbarkeit der einzelnen Elemente geachtet werden mußte.
Bei den Molekülen schließlich muß(te) es noch einige Modellkorrekturen geben, nicht so jedoch beim (geruchlosen) Stickstoff mit seiner besonders
großen Bindungsenthalpie. Die weiter oben angegebene Struktur mit zwei (nicht aromatischen!) 6-Elektronenringen, ist im Gegensatz zu Ethen und Ethin, “quasi aromatisch” riechenden Molekülen, deshalb stabil, weil die
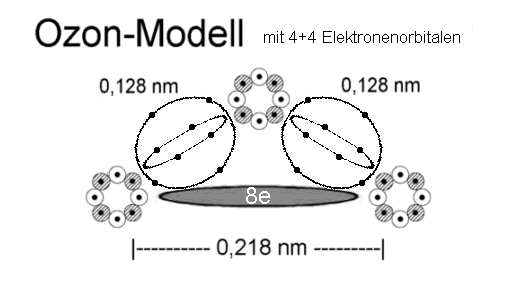
ineinander verschränkten Elektronenringe das Stickstoffmolekül hier fest umschließen, - vergl. etwa obiges Ozon-(und Ethin-)molekül sowie andere
Moleküle, mit eher lose gebundenen inneren / äußeren Elektronenringen. etwa bei dem unten abgebildeten korrigierten Ozonmodell
>>> In der Kolumne “Mathematische Fiktionen” bdw-01/2020 beschreibt Frau S. Hossenfelder die absurden Irrtümer am LHC
und das komplette Versagen der quantenmechanischen Voraussagen. Trotzdem weiter so?!
|