|
Kernmechanische Orbitale
Wenn man die dem Kernmechanischen Modell zugrunde liegenden Thesen im einzelnen kritisch überprüft - was man gelegentlich auch bei der konkurrierenden “klassischen” Quantenphysik, der Quantenmechanik,
immer mal wieder tun sollte - , dann gibt es hier wie dort sicher Punkte, die in besonderem Maße Anlaß zu Zweifeln geben können: Bei der Quantenmechanik wäre das zum Beispiel der genaue (in der Kernmechanik ganz reale) Hintergrund und Stellenwert der sogenannten Unschärferelation und bei der Kernmechanik ist es etwa die alternative parallele Anordnung der (8er-)Kernringe beim O-16- und Mg-24-Nuklid, sowie die dortige unterschiedliche Ausrichtung von Kernspin und Dipolmoment der Nukleonen!
Das Kernmechanische Modell führt ja die quantenmechanische, in sehr kleinen Dimensionen stets anzutreffende fundamentale Unschärfe nun eben darauf zurück, daß alle im Atom vorkommenden Elementarteilchen wie Protonen, Neutronen, Elektronen, Photonen, sowie deren Antiteilchen sich auf genau definierten Bahnen,- bei Abwesenheit sonstiger Felder: auf – durch Neutrinos und Teilchenspin bewirkten – Kreisbahnen, jeweils um ihren eigenen (zeitlich gemittelten, eigentlich aber leeren) virtuellen Schwerpunkt bewegen. Ein analoges Beispiel hierzu wäre etwa ein großer auf dem Wasser treibender luftgefüllter Ball, der von einem langsam im Kreis drehenden Wind im Idealfall ebenfalls auf eine Kreisbahn gezwungen wird;- mit dem Unterschied, daß bei den Elementarteilchen nicht der “Neutrinowind” ständig dreht, sondern durch den Teilchenspin lediglich der (für 0 und 180° natürlich unterschiedlich große) Wirkungsquerschnitt.
Wenn nun, wie zuletzt dort vermutet, beim Mg-24-Nuklid zwei von den drei 8er-Kernringen parallel als “Sandwich” angeordnet wären, sollte dies ja
dann gleichermaßen ebenso für S-32 und, anders als in der Fig. 1 dargestellt, auch für O-16 gelten! Aus verschiedenen Gründen macht dies aber keinen Sinn, da das Modell dann entweder bei der Kernform,
beim Dipolmoment oder den (jeweils vom Kern abgeleiteten) chemischen Bindungen – man vergleiche die aufgeführten Beispiele mit C(!) und O – nicht mehr richtig paßt.-
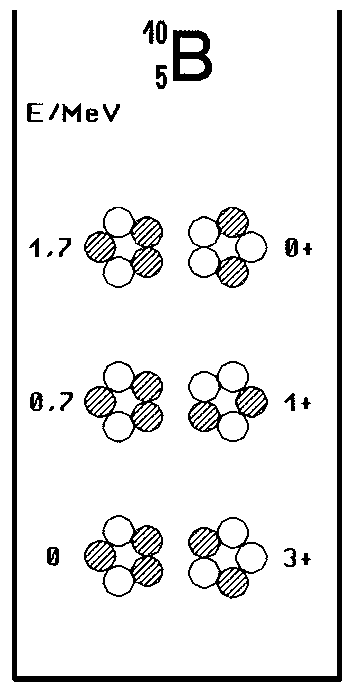
Ein Gutes hat der keineswegs unnütze Umweg, s. a.: Zitate+Aphorismen, letztendlich aber doch: Beim zunächst gar nicht gemeinten B-10-Kern, Fig. 2, stimmt das Modell dafür jetzt nämlich gleich umso besser. Das gilt einmal für das Termschema selbst und die dort aufgeführten Konfigurationen, insbesondere, was den zweiten angeregten Zustand mit 0+ anbelangt. Zum anderen ergibt sich bei
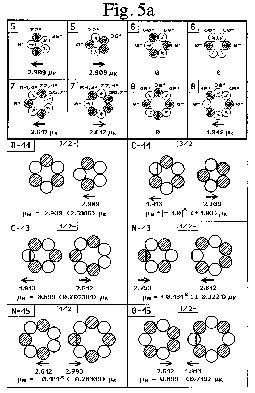
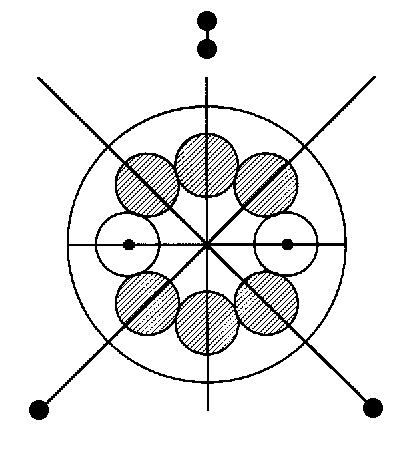
paralleler Anordnung der Kernringe im Grundzustand für das Dipolmoment nunmehr auch dann (und nur dann?) das auf ein Promille genaue Ergebnis (als Vektoraddition der Einzelmomente beider Kernringe, Fig. 5, im Winkel von 2x 72°), wenn, wie es eigentlich ohnehin normal erscheint, Spin und Dipolmoment der Nukleonen ebenso parallel aneinander gekoppelt und dabei tangential zum Ring gerichtet sind!
D. h., vieles spricht nunmehr dafür, daß die beim Kernmechanischen Modell lange gepflegte Annahme der radial zu den Kernringen
orientierten Nukleonen-Momente damit generell nicht mehr aufrecht erhalten werden kann. Dementsprechend müßten alle in der Fig. 5 eingezeichneten Vektorpfeile gleichfalls korrigiert und um 90° gedreht
werden, wodurch sich das Gesamtmoment eines jeden Kernringes zwar nicht in seinem Betrag, wohl aber in seiner Ausrichtung (90°-Drehung in der Ringebene) ebenso ändern würde.
Zu beachten ist noch: Einzig im Fall von B-10 bleibt, da sich alle Änderungen in der Summe wieder
aufheben, die Gesamtbilanz letztlich gerade unverändert. Das gilt sogar auch für die oben erwähnte Darstellung in der Fig. 2. Man muß sich dabei nur vergegenwärtigen, daß nun die beiden (hier:
5er-)Kernringe nicht wie bei C-12 oder O-16 ineinander verschränkt sind, sondern – Nukleon auf Lücke und umgekehrt – jetzt einfach als “Sandwich” übereinander liegen.
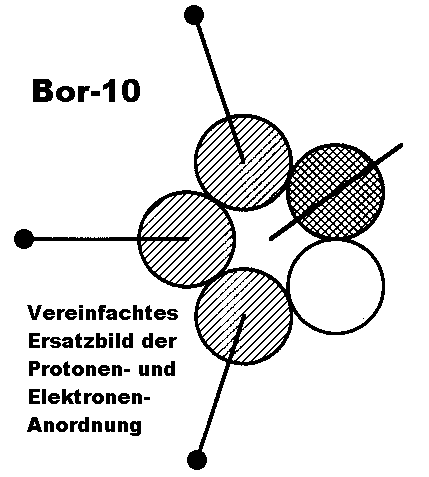
Der besseren Übersichtlichkeit wegen kann man nun noch (in der Anschauung) die Protonen des einen Kernrings auf den anderen übertragen,
um dann auf der “gegenüberliegenden” Seite quasi freie Neutronenplätze mit Protonen aufzufüllen. Das so erhaltene vereinfachte Ersatzbild der Protonenanordnung in einem (5er-)Ring – drei benachbarte Positionen sind mit einem Proton besetzt, eine doppelt und eine bleibt frei – enthält damit beim Kernmechanischen Modell definitionsgemäß alle notwendigen Informationen zur Ableitung der hiervon abhängigen Elektronenbahnen (Orbitale) des entsprechenden Atoms oder Moleküls.
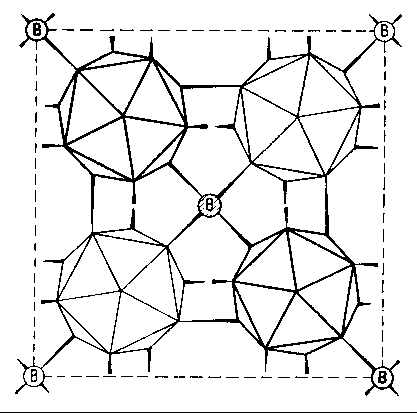
Im Fall von B-10 kann man sich an Hand der für Bor charakteristischen Ikosaeder-Grundstruktur sehr eindrücklich davon
überzeugen, daß das Modell an dieser Stelle “auffallend” stimmt. Außerdem bestätigt es ebenfalls noch die frühere Vermutung, daß das verbindende mittlere “Boratom” zwischen jeweils vier B12-Ikosaedern beim tetragonalen Bor I in Wirklichkeit nur ein Kohlenstoffatom sein kann.
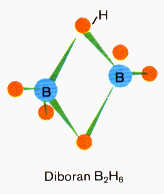
Etwas schwieriger ist da schon die genaue Aufklärung und Begründung des aus zwei (allein nicht “lebensfähigen”) BH3-Gruppen
zusammengesetzten Diboran, einer sogenannten Elektronenmangel- oder Dreizentrenbindung, wo sich zwei Wasserstoffatome ihr Elektronenpaar mit den Boratomen teilen. Tatsächlich m u ß das Kernmechanische Modell ja nun auch erklären, wie es möglich ist, daß das gänzlich anders aufgebaute Boratom dennoch nach Art des Kohlenstoffs vier “annähernd” in die Ecken eines Tetraeders weisende Bindungen zugleich bedienen kann
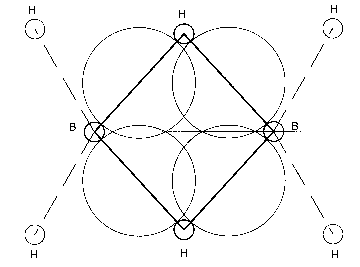
Daß die jeweils äußeren zwei Wasserstoffatome sich mit gemessenen 121,5° von den
ursprünglichen 144° des Kernringes entfernt und mehr dem Tetraederwinkel von 109,5° angenähert haben, ist sozusagen noch klassische Chemie. Für die mittleren H-B-H-Winkel in Höhe von 97° gibt es aber nur
eine mögliche Erklärung im Rahmen des Kernmechanischen Modells, die plausibel erscheint: In der – winkelhalbierenden – Ebene, genau zwischen den beiden oben erwähnten Orbitalen zu den äußeren
Wasserstoffatomen, befinden sich nunmehr genau vier, mit jeweils nur einem Elektron besetzte Orbitale* von ca. 1,1 nm Durchmesser, welche sich gegenseitig wahrscheinlich leicht überlappen, aber demnach
gerade dazu geeignet sind, den Abstand von 1,33 nm zwischen B- und H-Atomen (außen übrigens 1,19 nm) zu überbrücken; s. Abb., rechts.
Während das Boratom also über drei eigene Bindungselektronen verfügt, sind es beim Kohlenstoff typischerweise (mindestens) vier. Die
klassische Quantenmechanik rechnet im Grundzustand dabei zunächst nur mit zwei bindungsfähigen Elektronen. Sie gewinnt dann die zwei weiteren (zu den ersten beiden tatsächlich absolut gleichwertigen) Elektronen erneut – wieder einmal – erst durch einen eigens dafür ersonnenen mathematischen Kunstgriff: Die sogenannte sp3-Hybridisierung des Kohlenstoffatoms, welche diesen Trick bewirken soll, verdankt ihre wundersame Existenz nämlich in keiner Weise der Quantenmechanik,
sondern es ist genau umgekehrt. Deren Existenz wurde in Wirklichkeit vielmehr erst durch die Anpassung der Theorie an die beobachtete Bindungsgeometrie gerettet. Da berührt es dann schon seltsam, wenn
stereotyp immer wieder beschwörend von Hybridisierung, Delokalisierung oder Mesomerie der Valenzelektronen die Rede ist, um ein – gar nicht vorhandenes – tieferes Verständnis lediglich vorzutäuschen und dann auch noch die Theorie für ihre bemerkenswerte Anpassungsfähigkeit zu loben.
Bei der im Sinne des Wissenschaftstheoretikers Karl Popper an jeder Stelle falsifizierbaren alternativen Kernmechanik ist das grundlegend anders. Das Kernmechanische Modell m u ß wie gesagt immer wieder aufs Neue beweisen, daß seine Aussagen für ein bestimmtes Molekül auch tatsächlich zutreffen.
Natürlich ist es da ebenfalls möglich, daß bereits die – zunächst – angenommene Kernstruktur falsch ist, wie das obige Beispiel mit dem
Boratom zeigt. Genau das macht es der neuen Theorie am Anfang so schwer, ihre Richtigkeit zu beweisen. Zugleich ist dies aber auch eine ungeheure Chance, den genauen Aufbau der Atomkerne nun im
Umkehrschluß an Hand der leichter zugänglichen chemischen Bindungen zu überprüfen.
Besonders gut gelungen ist das auf Anhieb beim für die moderne Chemie nicht ganz unwichtigen Kohlenstoffatom,
dessen ungeheure Bindungsvielfalt mit einfachstem “Kerndesign” erzielt wird. Setzte übrigens das Boratom in seinem Erscheinungsbild ganz auf das Signet der Firma Chrysler, ohne als langjähriger
Vorbenutzer des Copyrights etwas dafür zu bezahlen, so fehlen einem für die schon seit Jahrmilliarden andauernde Verwendung gleich zweier Mercedessterne am Ende die Worte,- aber genau das praktiziert das C-Atom mit “seinem” doppelten Markenzeichen.
Man sieht nun sofort, daß – anders als beim Bor, Sauerstoff und Stickstoff – kein einziges KMO (Kernmechanisches Orbital, englisch: NMO für Nuclear
Mechanical Orbital) hier doppelt besetzt ist. Gerade dies aber ermöglicht es dem Kohlenstoff, nach Belieben zwischen den (in der Regel zwei) kerngebundenen “s”-Elektronen und den nicht um den Kern kreisenden Valenzelektronen zu wechseln: Beim Diamanten betätigen alle vier nicht axialen Elektronen die Bindungen des Diamantgitters, während es bei CO2 nur die beiden(!) axialen sind, welche tatsächlich die Bindung bewirken. Allerdings sind auch die beiden anderen nicht axialen Valenzelektronen letztlich doch noch mitbeteiligt,- in dem sie nämlich zum stark elektronegativen Sauerstoffatom überwechseln.
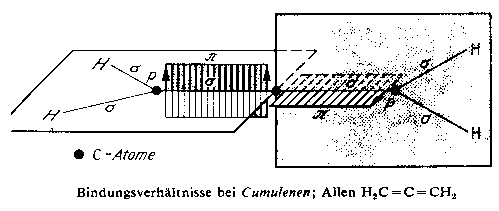
Bei den sogenannten nicht gesättigten Doppelbindungen des Kohlenstoffs sind sogar alle drei von einem Kernring bestimmten Orbitale (siehe: Mercedesstern)
beteiligt, weil hier nämlich die seitlichen (Pi-)Bindungen allein nicht stabil wären. So muß deshalb in diesem Fall also erst noch zusätzliche Energie aufgebracht werden, um ein axiales “s”-Elektron für
die unbedingt notwendige zentrale (Sigma-)Bindung aus der kernzentrierten Orbital-Bahn zuvor entsprechend anzuheben.
Auch bei den aromatischen Verbindungen des Kohlenstoffs, insbesondere beim jetzt beschriebenen Benzol(-ring),
sind ebenfalls alle drei zu einem Kernring gehörenden Elektronen (allerdings an jeweils unterschiedlichen Bindungen) beteiligt: zweimal im Ring zum benachbarten Atom und einmal zum äußeren
Wasserstoffatom. Die zwei nicht axialen Elektronen des anderen Kernrings befinden sich im Grundzustand.- Bleibt also – bei jedem Kohlenstoffatom – noch ein weiteres freies axiales Elektron, dessen
Orbital folglich gerade in der Ringebene liegt.
Nach der klassischen Quantenmechanik kreisen alle sechs Elektronen gemeinsam im Ring und erhöhen so durch ihre “Resonanzenergie” noch zusätzlich die Stabilität des Benzols.- “Warum
sind aromatische Verbindungen stabil?” fragt ebenfalls Jun-ichi Aihara in Spektrum der Wissenschaft von Mai 1992 auf S. 64-71 und beschreibt dabei zugleich ein eigenes theoretisches Berechnungsmodell.
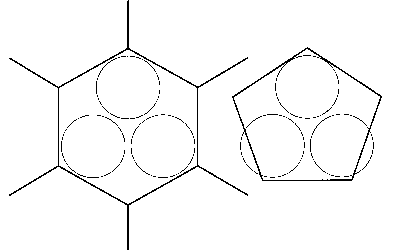
Nach dem Kernmechanischen Modell ist es noch einfacher, weil ja hier freie Elektronen auch unabhängig von einem zentralen Kern ohnehin ständig kreisen. Geometrisch bedingt sind es genau drei doppelt besetzte Orbitale - oder aber analog zu Diboran, s.
Korrektur rechts oben - ebenfalls ein einziger Orbitalring mit sechs Elektronen, der nunmehr gerade im freien Innenraum von Aromaten Platz findet. Gleiches gilt ebenfalls noch für das
Cyclopentadienyl-Ion, das zu den stabileren negativen(!) Ionen zählt.
Auch wenn man man auf einer Rastertunnelmikroskop-Aufnahme erst drei Orbitalringe im Inneren der Benzolringe zu sehen meint - es ist nur einer!
Gerd Schulte
Fortsetzung: Kernmechanisches Modell - neu und
Die chemischen Bindungen
|